Механохимические аппараты и методы оценки их эффективности: Учебное пособие, страница 18

Вернемся теперь к возможности использования времени установления равновесного гранулометрического состава при агрегации t_к для сравнения эффективности мельниц. В табл. 9 приведены значения t_к для WО₃ и МоО₃, механически обработанных в трех типах мельниц. Для сравнения здесь же представлены времена достижения равновесия Хюттига (t_x), S_max при диспергации (t) и максимальных величин поверхности при агрегации  ([45]).

Таблица 9

Значения различных критериев для оценки эффективности мельниц

Параметр	АГО-2		АПФ		FRITSCH
	MoO3	WO3	MoO3	WO3	MoO3	WO3
tx, c	17.5	6.9	32.3	16.9	421.3	81.6
t, c	14.6	5.6	32.6	20/1	397.0	78.4
tк, c	1200	300	3000	600	4000	1800
c	40.0	15.0	150	30.0	¥	150

Видно, что погрешность определения t_к очень велика, поскольку в данном случае необходимо проводить МО в течение ~1000 с и более, тогда как время достижения максимума функции S = S(t) при агрегации определяется со значительно меньшей погрешностью и намного быстрее. Таким образом, при наличии агрегации механически обрабатываемого материала наиболее адекватным параметром для сравнения эффективности мельниц является время достижения максимума функции S = S(t) –

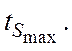
3.3. Модель агрегации

На основании детального рассмотрения зависимости гранулометрического состава от времени механической обработки оксидов молибдена и вольфрама в мельницах трех типов авторами [46] показано, что процесс агрегации самых мелких частиц происходит не сразу до какого-то определенного размера r_c, как это предполагалось ранее в работах [43, 58], а в несколько стадий. Схему процессов, происходящих при МО материалов, авторы [46] предлагают представить в виде диспергации исходных частиц пяти последовательных агрегаций и раскола последних (наиболее крупных) агрегатов на два осколка. При этом в случае агрегации каждый последующий агрегат образуется из предыдущих до размеров, в p @ 2.3 раз превышающих предыдущие:

   r_max ® r_min ® pr_min ® p²r_min ® p³r_min ® p⁴r_min ® p⁵r_min ®  r_min,                                                (23)

где r_max – средний радиус частиц исходного порошка, r_min – средний радиус частиц, достигших минимального размера, q @ 2.

Для описания процессов, описываемых схемой (23), была построена модель, названная авторами «Моделью с пятью слипаниями и расколом» [46]. Рассмотрим эту модель подробнее. Для построения модели был использован метод, описанный в разделе 3.1. В соответствии с рассуждениями, приведенными в этом разделе, число частиц радиусом r_max, не расколовшихся после i-го удара, равно

n_0i = n₁(1 – k₁)ⁱ = na(1 – k₁)ⁱ = nx₁,                        (24)

где 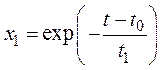; t = t₁ lna;

                  ;

;

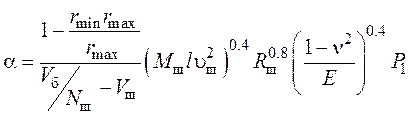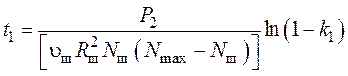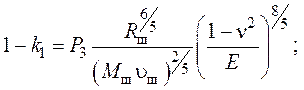
P₁, P₂, P₃ – const.

Тогда число частиц, расколовшихся до размера r_min, составляет  где 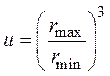. Следуя ранее принятому ходу рассуждений, предположим, что из n₂ частиц с радиусом r_min, попавших под удар, агрегируются только k₂n₂ (k₂ < 1) частиц в зоне удара, в которой развиваются давление и температура, приводящие к агрегированию до частиц размером pr_min. Тогда количество частиц, слипшихся до размера  равно:

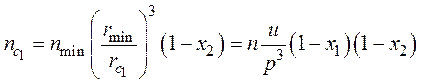    ,                    (25)

где  .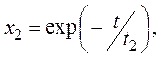

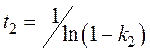Если из  частиц размером pr_min агрегируются только k₃(k₃ <1) частиц размером  = p²r_min, то их число равно:

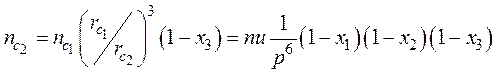    ,          (26)

где  .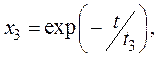

Аналогичное количество слипшихся частиц размером p³r_min из частиц размером p²r_min, частиц размером p⁴r_min из частиц размером p³r_min, частиц размером p⁵r_min из частиц размером p⁴r_min описывается соответственно выражениями:

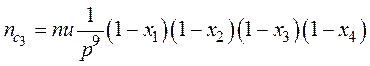     ,                          (27)

где  ;.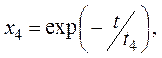

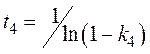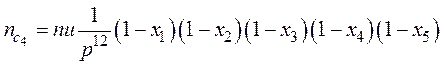     ,               (28)

где  ;.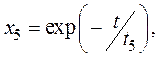

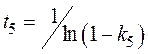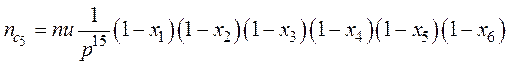     ,      (29)

где  .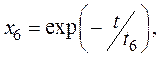

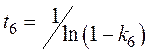Если размер p⁵r_min превышает предел Гриффитса, то эти частицы раскалываются на две части, размер каждой из которых меньше указанного предела. Тогда количество таких расколотых частиц равно