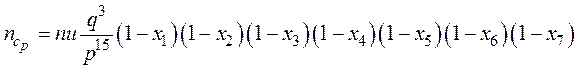Механохимические аппараты и методы оценки их эффективности: Учебное пособие, страница 19

, (30)

где  .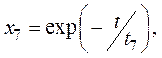

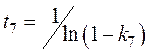Число не слипшихся частиц размером r_min, pr_min, p²r_min, p³r_min, p⁴r_min, p⁵r_min составляет соответственно:

     ;                                                       (31)

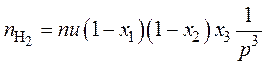     ;                                         (32)

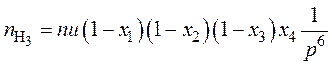    ;                                 (33)

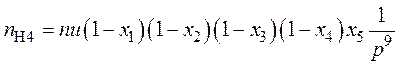     ;                     (34)

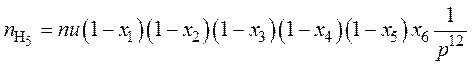     ;           (35)

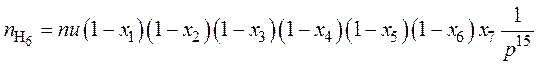     .  (36)

Тогда общее число частиц в системе будет складываться из:

      ,        (37)

где  – число неразрушенных частиц с исходным радиусом r_max.

Легко убедиться, что объем, занимаемый исходными частицами, равен объему частиц, вновь образованных, т. е.

   

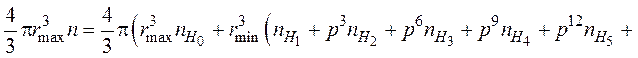
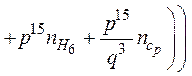     .                                                   (38)

Выше был описан метод, использованный авторами [43], определения величин t₁(t) и t₀ (с использованием начальных точек графика функции S = S_max [1 – exp( – (t – t₀)/ t₁)], построенного в логарифмических координатах). Следует напомнить, что при этом агрегация не учитывалась.

Для того чтобы вычислить величины t₂, t₃, t₄, t₅, t₆, t₇, рассмотрим конечное распределение частиц по размерам, которое устанавливается в некоторый момент времени t_к и при дальнейшей МО практически не меняется. Как отмечалось, t_к устанавливается экспериментально для каждого вещества и для каждой мельницы, и также является характеристикой эффективности мельницы. Числа l₀, l₁, l₂, l₃, l₄, l₅, l₆ обозначают число частиц с радиусами r_min, pr_min, p²r_min, p³r_min, p⁴r_min , p⁵r_min ,  r_min соответственно. Поэтому общий объем всех частиц равен

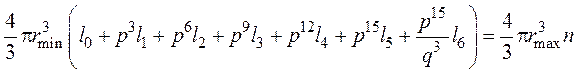  . (39)

Отсюда

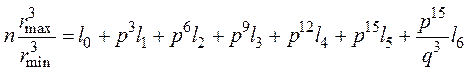     .            (40)

Для удобства дальнейшего изложения обозначим правую часть выражения (40) за , тогда

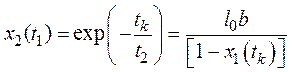    ,                                       (41)

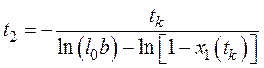    .                                          (42)

Аналогично

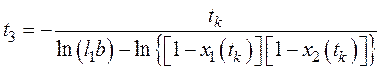     ;                        (43)

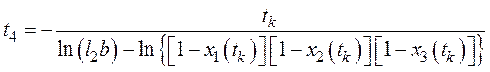     ;         (44)

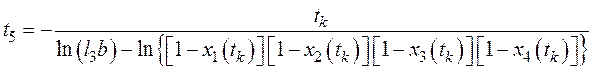;    (45)

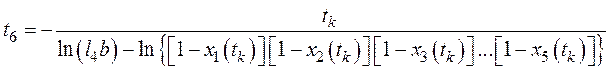; (46)

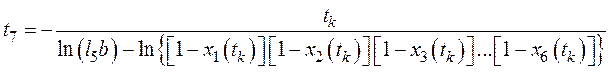. (47)

Вычислив таким образом значения t₀ , t₁, t₂, t₃, t₄, t₅, t₆, t₇ и определив затем величины x₁, x₂, x₃, x₄, x₅, x₆, x₇, можно в любой момент времени найти величину внешней поверхности порошка по формуле

             

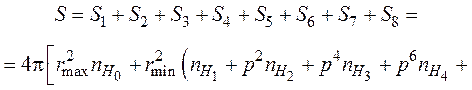
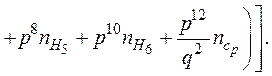                                            (48)

Таким образом, с использованием выражения (48) были определены кинетические зависимости S(t), из которых вычислено время достижения максимума величины поверхности, являющееся характеристикой эффективности мельниц. Аналогично определены максимумы величин отдельных слагаемых S₁ – S₈. Типичные кинетические кривые изменения этих величин во времени приведены на рис. 8.

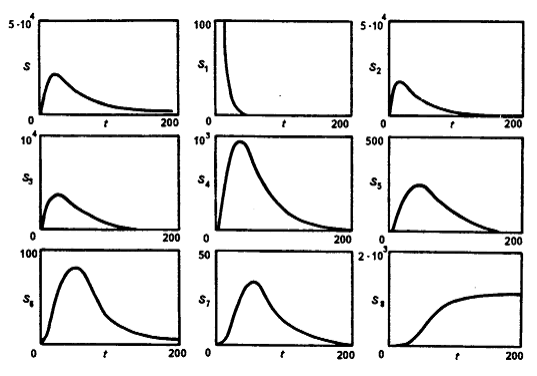
Рис. 8.Типичные кинетические кривые S(t), S₁(t), S₂(t), S₃(t),
S₄(t), S₅(t), S₆(t), S₇(t), S₈(t)

Для вычисления кинетических кривых S(t) сначала подбирались константы P₁ и P₂ параметров модели a и t₁ в выражении (24). Чтобы теоретически рассчитанные величины a и t₁ совпадали со «стандартными «(экспериментально полученными значениями), при расчете использовались экспериментальные значения t_k и l_i . В результате вычисления кинетической кривой S(t) для стандартных (экспериментальных) условий МО в мельницах трех типов определено время достижения максимальной поверхности , которое хорошо согласуется с экспериментально полученным  (табл. 10). Здесь же для сравнения приведены значения , вычисленные с помощью «модели с одним слипанием» (по сокращенной схеме (23), учитывая только три первых слагаемых в выражении (48)).

Таблица 10

Параметры модели для оксида молибдена в различных аппаратах в «стандартных» условиях

Параметр	АГО-2	АПФ	FRITSCH
с	40.0	150.0	¥
, с	41.0	148.0	»200
, с а)	38.4	120.0	¥
tk, c	1200.0	3087.0	3969.0

 

Примечание

^а) Значения, полученные с использованием модели «с одним слипанием».

Кроме того, рассчитаны кинетические кривые при варьировании условий МО в трех различных мельницах. Характеристики этих кривых приведены в табл. 11–14, где наряду с величинами , приведены теоретические значения максимальной величины поверхности S_max, отнесенные к исходной величине поверхности. Это отношение позволяет оценить изменение внешней поверхности в результате МО.