Промышленность \ Промышленная экология

Механохимические аппараты и методы оценки их эффективности: Учебное пособие, страница 14

Примечание

а) Здесь и далее в табл. 15 rmax = 35 мкм, rmin = 0.2 мкм,  г/см3.

б) Стандартные условия:

в АГО-2: Rш = 0.4 см, Nш = 95 шт, Мм = 5 г, rш = 7.9 г/см3, uш = 9.58 м/с; Vб = 145 см3;

АПФ: Rш = 0.4 см, Nш = 476 шт, Мм = 50 г, rш = 7.9 г/см3, uш = 7.34 м/с; Vб = 639 см3;

FRITSCH: Rш = 1.0 см, Nш = 18 шт, Мм = 10 г, rш = 4.0 г/см3, uш = 5.69 м/с, Vб = 589 см3.

Эти величины рассчитаны по экспериментальным данным, полученным ранее [43]. Поэтому значения скорости в «стандартных» условиях совпадают с экспериментальными. Таким образом, используя экспериментально определенные ранее [43] параметры a и t и полученные выражения (20), (21), можно найти константы, с точностью до которых эти выражения соответствуют эксперименту, и определить значения a и t для каждой мельницы. Далее можно рассчитать скорости достижения максимальной величины внешней поверхности в различных режимах работы мельниц без предварительного эксперимента.

В табл. 5 приведены численные значения параметров модели u и t0 для оксида вольфрама, механически обработанного в мельнице АГО-2, в зависимости от его исходных характеристик (массы загрузки вещества в барабан и исходного размера частиц). Видно, что изменение указанных характеристик не влияет на величину скорости диспергации.

Таблица 5

Расчетные параметры моделиа) в зависимости от характеристик WO3, обрабатываемого в мехактиваторе типа АГО-2б)

Параметр

Мм, г при rmax = 20 мкм

rmax, мкм при Мм = 5 г

2.5

5.0в

20.0

2.0

5.0

u, с-1

0.18

0.18

0.18

0.18

0.18

T0, c

1.4

1.4

1.4

0.8

1.2

Tx, c

6.9

6.9

7.1

6.4

6.8

Примечание

Здесь и далее в табл. 11, 12

а) При  г/см3, rmin = 0.2 мкм, k = ((1-n2)/E)2/5 = 1.65×10-2 ;

б) Режим работы мельницы АГО-2 здесь и далее см. табл. 10.

в) Экспериментальные условия, принятые за стандартные.

В табл. 6–8 приведены экспериментальные и расчетные значения u и t0 для оксида вольфрама при его МО в трех типах мельниц в различных условиях диспергации. При этом поочередно варьировались величины: Rш , Nш, Mш ,uш и rш .

Преобразуя (21), получаем выражение

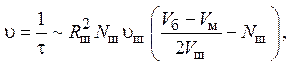                                           (22)

анализ которого показывает, что при 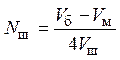 значение u максимально, и, следовательно, данное количество шаров является оптимальным. Оптимальные значения количества шаров Nопт при разных радиусах шаров приведены в табл. 4, 6–8. В табл. 6–8 также приведены значения скорости u при оптимальном количестве шаров. Видно, что максимальная скорость диспергации в большинстве случаев достигается при меньшем радиусе шаров.

При условии сохранения постоянства числа шаров, с изменением их радиуса, выражение (22) можно привести к виду: 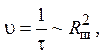 откуда следует, что скорость диспергации должна возрастать с увеличением радиуса шаров. В действительности при неизменном числе шаров возрастание скорости наблюдается, наоборот, при уменьшении радиуса шаров. Это, очевидно, связано с тем, что при уменьшении радиуса шаров величина 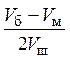 возрастает быстрее, чем уменьшается . Увеличение скорости диспергации связано с числом шаров, необходимым для полного заполнения барабана: чем меньше радиус шара, тем это число больше, т. е. 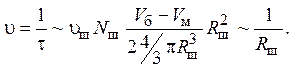 Действительно, при малом (Nш~0) и большом (Nш~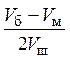) числе шаров наблюдается зависимость  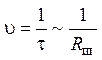(см. табл. 5–7), при числе шаров, близком к оптимальному, (Nш~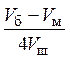) – 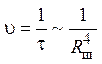, что и продемонстрировано в таблицах.

Увеличение массы диспергируемого вещества всегда приводит к уменьшению скорости диспергации согласно формуле (22).


Таблица 6

Расчетные параметры модели а) в зависимости от условий механической обработки оксида
вольфрама в АГО-2

Скачать файл