Механохимические аппараты и методы оценки их эффективности: Учебное пособие, страница 12

3.1. Модель диспергации

Увеличение удельной поверхности порошков твердых веществ путем измельчения в мельницах с целью повышения скорости какого-либо процесса (каталитической активности, спекания, экстракции и т. д.) является непременной стадией многих химических технологий создания новых материалов. Измельчение твердых тел – довольно энергоемкая операция, поэтому даже небольшое увеличение эффективности может дать ощутимый экономический эффект. Для описания процессов измельчения вещества предложена модель диспергации [46], в которой все параметры приводятся в аналитическом виде и выражаются как функции от числа шаров, их массы, радиуса и скорости, от объема барабана, от начальных и конечных размеров частиц твердого вещества и от их механических параметров (модуля Юнга и коэффициента Пуассона). Выполненные с помощью данной модели расчеты позволили найти оптимальные условия для измельчения вещества в аппаратах АГО-2, АПФ и FRITSCH и сравнить эффективность их воздействия.

При построении модели был использован постулат, предложенный в работе [23], о замене большого числа различающихся по интенсивности и длительности импульсов механического воздействия на то же количество импульсов со средней интенсивностью и длительностью.

Рассмотрим конкретную модель бинарных столкновений N_ш шаров радиусом R_ш со средней скоростью u_ш в объеме барабана V_б . Предположим, что в начальный момент времени обрабатываемый материал состоял из n частиц со средним радиусом r_max , причем при ударе эти частицы раскалываются на частицы со средним радиусом r_min. Такой подход обоснован известным фактом [49, 50], что диспергация приводит к двухпиковой картине распределения частиц по размерам.

Модель, предлагаемая в работе [23], допускает, что все частицы радиусом r_max, попадая под удар, раскалываются на частицы радиусом r_min. Чтобы учесть влияние силы механического воздействия и механических параметров обрабатываемого материала, предположим (рис. 4), что из n₁ частиц радиусом r_max, попадающих под удар, только k₁n₁ частиц раскалываются до радиуса r_min, где k₁ < 1.

Величина k₁ определяется [51] из отношения количества частиц, попавших под удар в зоне площадью S₁ (рис. 4) и расколовшихся n к общему числу частиц, попавших под удар в зоне площадью S₀

k₁ = n_p / n₁.                                   (4)

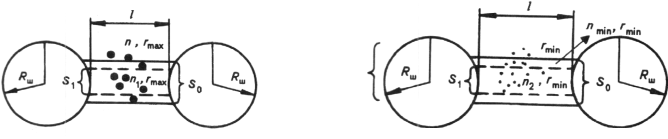
Рис. 4. Схема соударения шаров и частиц материала при механической обработке

Допустим, что n частиц радиусом r_max, как и шары, распределены по всему объему барабана равномерно, тогда плотность частиц в свободном объеме распределяется как r = n/V_св , где V_св = V_б – V_ш , V_б – объем барабана, V_ш – объем шаров, равный 4/3 p R_ш³ N_ш. Тогда число попавших под удар частиц n₁ описывается выражением

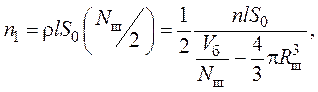                                              (5)

где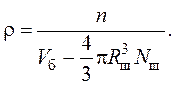

Число частиц, не расколовшихся после первого удара и попавших в пространство вне зоны S₁, но в пределах зоны S₀ (рис. 4) равно n₀₁ =
= n₁ – k₁n₁ = n₁ (1 – k₁), после второго удара – n₀₂ = ₁ (1–k₁) – k₁ (n₁ (1–k₁)) = = n₁ (1–k₁)², после i-го удара –

n_0i = n₁(1-k₁)ⁱ.                                 (6)

Согласно кинетической теории газов [52] число ударов за 1 с равно z = 1/q ~ R²uN ², тогда число ударов за время t равно i = t/q. В данном случае вместо N  ² следует взять величину 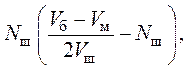 учитывающую вместимость барабана (V_м – объем материала). Действительно, соударений шаров не будет, если N_ш = 0, либо V_б = V_м, либо N_ш = N_max = 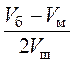). Отсюда число нерасколовшихся частиц равно

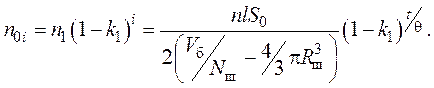                              (7)

Так как общее количество частиц состоит из совокупности исходных и расколовшихся, следовательно, в целом площадь внешней поверхности равна

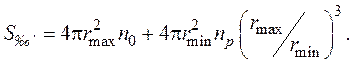                                          (8)

Полагая, что n_p = n – n₀ , получим

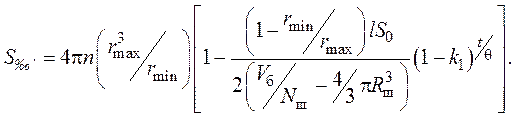                  (9)

В случае, если расколов нет, r_max = r_min и S_вн = 4.

Обозначая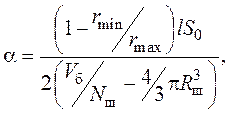

            

                                       

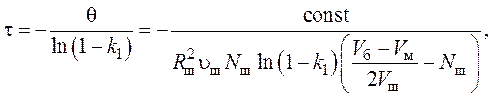
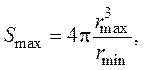
получаем выражение для расчета площади внешней поверхности с параметрами модели a и t:

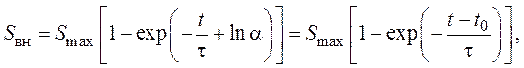                 (10)

где t₀ = tlna.