F= -mg sin α![]()
При малых углах отклонения (а мы будем изучать колебания только с малыми углами отклонения)
![]() sin α ≈
sin α ≈ ![]()
Поэтому
F=
-mg![]() = -
= - ![]() x
x![]()
Величина
![]() - постоянна. Обозначим её через k. Тогда
- постоянна. Обозначим её через k. Тогда
F= -kx
Таким образом, несмотря на то, что колебания идеального пружинного маятника и математического маятника вызываются силами, имеющими разную природу (сила тяжести и сила упругости), закон изменения возвращающей силы одинаков. Подмеченная закономерность является характерным признаком колебательной системы, в которой свободные колебания являются гармоническими.
Она состоит в том, что возвращающая сила пропорциональна смещению колеблющегося тела от положения равновесия и всегда направлена в сторону равновесия. Так как по второму закону Ньютона
F=ma,
то
Эта связь между мгновенными значениями ускорения и смещения тела является основным уравнением гармонических колебаний.
2 Энергетические преобразования при свободных колебаниях. Отведём маятник (рис. 8) на небольшой угол а из положения устойчивого равновесия. Этим мы сообщим маятнику дополнительную потенциальную энергию
Wп = mghm
где hm - максимальное значение высоты подъёма маятника. Отпустим маятник. Под действием поля тяготения и силы упругости нити маятник будет двигаться к положению равновесия. При этом его потенциальная энергия превращается в кинетическую. В положении равновесия вся сообщённая маятнику потенциальная энергия превратится в кинетическую (рисунок 8):
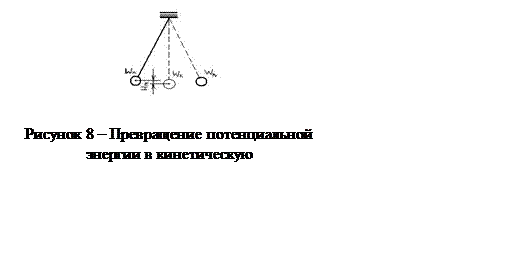 |
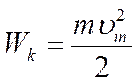
Где vm - максимальное значение скорости движения тела, подвешенного к нити. Дойдя до крайнего левого положения, маятник начнёт двигаться в обратном направлении. Энергетические преобразования при этом повторяются.
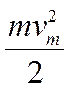 При
отсутствии сил трения по закону сохранения энергии максимальное значение
потенциальной энергии равно максимальному значению кинетической энергии:
При
отсутствии сил трения по закону сохранения энергии максимальное значение
потенциальной энергии равно максимальному значению кинетической энергии:
mghm =
Итак, при колебаниях маятника происходит периодическое
превращение потенциальной энергии в кинетическую и кинетической в потенциальную:
Wп → Wк → Wп → Wк→ Wп …
Интересно отметить, что за один период колебаний маятника
происходит два цикла превращения энергии. По закону сохранения и превращения энергии сумма кинетической и потенциальной энергии маятника остаётся постоянной:
E = Wк+ Wп = const
В крайнем положении кинетическая энергия маятника равна нулю, а потенциальная энергия максимальна и равна его полной энергии:
E = mghm
Для
того чтобы подсчитать полную энергию маятника, опишем вокруг точки подвеса
окружность радиусом, равным длине маятника l
(рисунок 9). Продолжим линию подвеса маятника в положении равновесия до
пересечения с окружностью в точке D. Соединим точку D с
точкой B. Нетрудно доказать, что образовавшийся при этом
треугольник ABC подобен треугольнику BCD(оба они
прямоугольные и имеют равные углы при вершинах B b D) Из подобия треугольников следует пропорциональность
их сходственных сторон:
 |
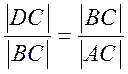 |
или
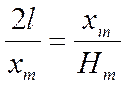 |
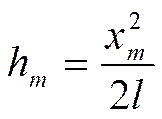 откуда:
откуда:
Подставив значение Hm в формулу E = mgHm,получим:
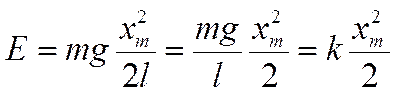 |
,
где 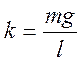 -
постоянная величина.
-
постоянная величина.
Мы видим, что полная энергия маятника пропорциональна квадрату амплитуды его максимального смещения:
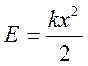
В случае пружинного маятника его кинетическая энергия в крайнем положении равна нулю, а потенциальная имеет максимальное значение и равна полной энергии маятника:
 |
Заменив в этой формуле возвращающую силу по закону Гука через Fm=kxm, получим:
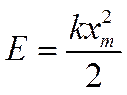 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.