Гармонические колебания, уравнения, график, параметры. Электромагнитные свободные колебания. Автоколебания, страница 11

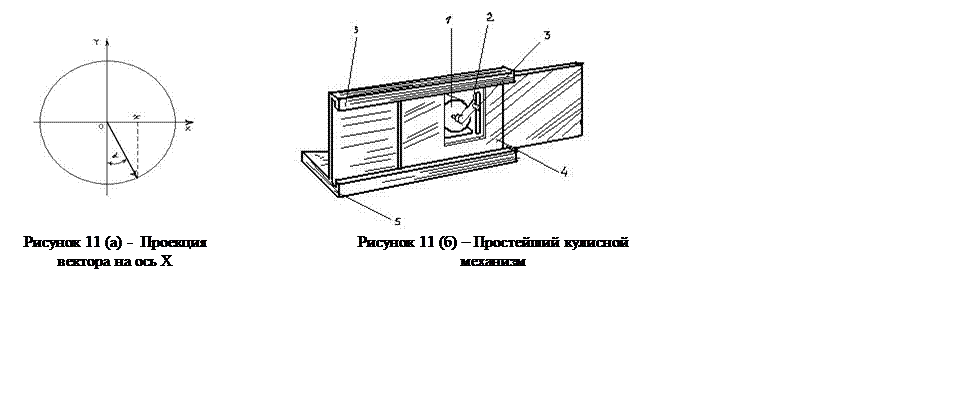
     4   Кинематическая связь между круговым движением и гармоническим колебательным движением. Пусть точка движется по окружности радиуса  R с постоянной угловой скоростью ω. Тогда проекция x-радиус – вектора этой точки на горизонтальную ось OX (рис.11, а) выразится так:

                                               x = R sin α

Но α = ωt. Поэтому:

      x = R sin ωt

Это значит, что проекция точки, движущейся по окружности, на ось OX совершает гармонические колебания с амплитудой x_m = R и циклической частотой ω. Это используется в так называемом кулисном механизме, предназначенном для преобразования вращательного движения в колебательное. Рассмотрим устройство кулисного механизма на простейшей его модели (рис.11б). На оси электродвигателя 1 укреплён кривошип 2, а на кривошипе – палец 3. При работе двигателя палец движется по окружности радиуса R. Палец вставлен в прорезь кулисы 4, которая может двигаться по направляющим 5. Поэтому палец давит на кулису и заставляет её смещаться то

вправо, то влево. Кулиса приходит в колебательное движение. Колебания кулисы – гармонические, так как прорезь в кулисе как бы проецирует движение пальца на горизонтальную ось.

Фаза колебаний. Разность фаз

     1   Понятие фазы колебаний. Так как  амплитудные значения смещения (x_m), скорости (υ_m) и ускорения(a_m) при гармонических колебаниях постоянны, то мгновенные значения этих величин, как видно из формул смещения, скорости и ускорения, определяются значением аргумента

φ = ω₀t,

называемого фазой колебаний.

     Таким образом, фазой колебания называется физическая величина, определяющая (при данной амплитуде) мгновенные значения смещения, скорости и ускорения.

Из формулы

x = x_m sin ω₀t

видно, что при t = 0 смещение x также равно нулю. Но всегда ли будет так?

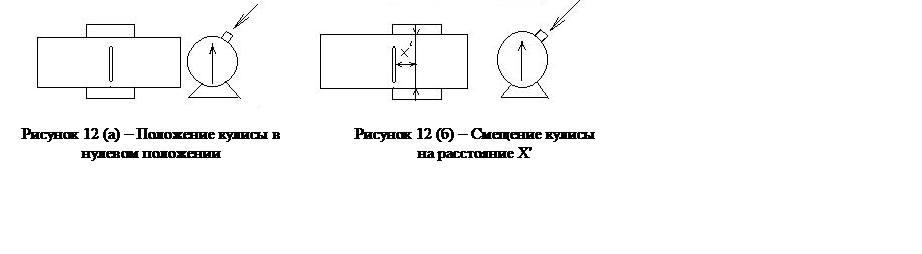
Допустим для конкретности, что мы наблюдаем движение кулисного механизма, отсчитывая время по положению стрелки секундомера. В этом случае момент t= 0 есть момент пуска секундомера. Запись «x = 0 при t= 0» означает, что секундомер был пущен в один из тех моментов, когда кулиса находилась в среднем (нулевом) положении (рис. 12, а). В этом случае

x = x_msin ω₀t

Предположим теперь, что секундомер был включен тогда, когда кулиса уже сместилась на расстояние x’ (рис. 12, б). В этом случае смещение кулисы через промежуток времени t, отмеченный секундомером, определится формулой

x = x_m sin ω₀(t + t^')

где t^' – время, необходимое на смещение кулисы на величину x’.

Преобразуем эту формулу

x = x_m sin (ω₀t + ω₀t^'),

или

x = x_m sin (ω₀t + φ₀),

 где φ₀  = ω₀t- начальная фаза колебаний. Мы видим, что начальная фаза зависит от выбора начала отсчёта времени. Если начало отсчёта времени ведётся с момента, когда смещение равно нулю(x = 0 ), то начальная фаза равна нулю. Изменение мгновенного значения

смещения в этом случае описывается формулой

x = x_m sin ω₀t

Если же за начало отсчёта времени берётся момент, когда изменяющееся смещение достигло наибольшего значения x = x_m, то начальная фаза равна π/2 и изменение мгновенного значения смещения описывается формулой

x = x_m sin (ω₀t + ) = x_m sin ω₀t

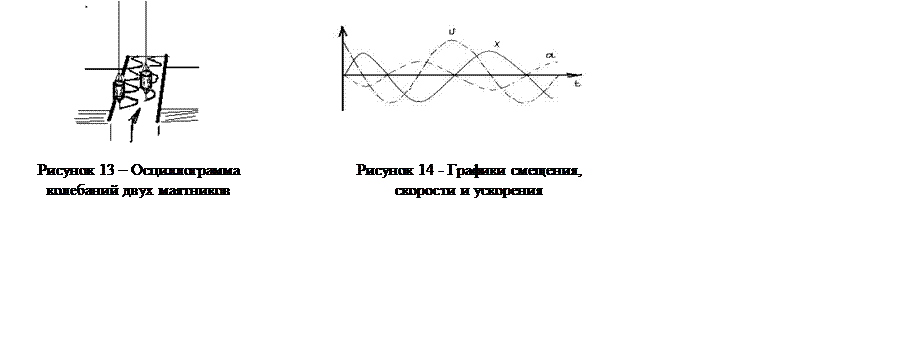
2 Разность фаз двух гармонических колебаний.Возьмём два одинаковых маятника. Подтолкнув маятники в разные моменты времени t₁ и t₂, запишем осциллограммы их колебаний (рисунок 13). Анализ осциллограмм показывает, что колебания маятников имеют одинаковую частоту, но не совпадают по фазе. Колебания первого маятника опережают колебания второго маятника на одну и ту же постоянную величину.

Уравнения колебаний маятников запишутся так:

x₁ = x_m sin (ω₀t + φ₁),

x₂ = x_m sin (ω₀t + φ₂)

Величина φ₁-φ₂ – называется разностью фаз или сдвигом фаз.

Из осциллограммы видно, что перенос начала отсчёта времени не изменяет разности фаз. Следовательно, разность фаз гармонических колебательных движений, имеющих одинаковую частоту, не зависит от выбора начала отсчёта времени. На рисунке 14 представлены графики смещения, скорости и ускорения для одного и того же гармонически колеблющегося тела. Как видно из рисунка, колебания этих величин происходят с различными начальными фазами.