 |
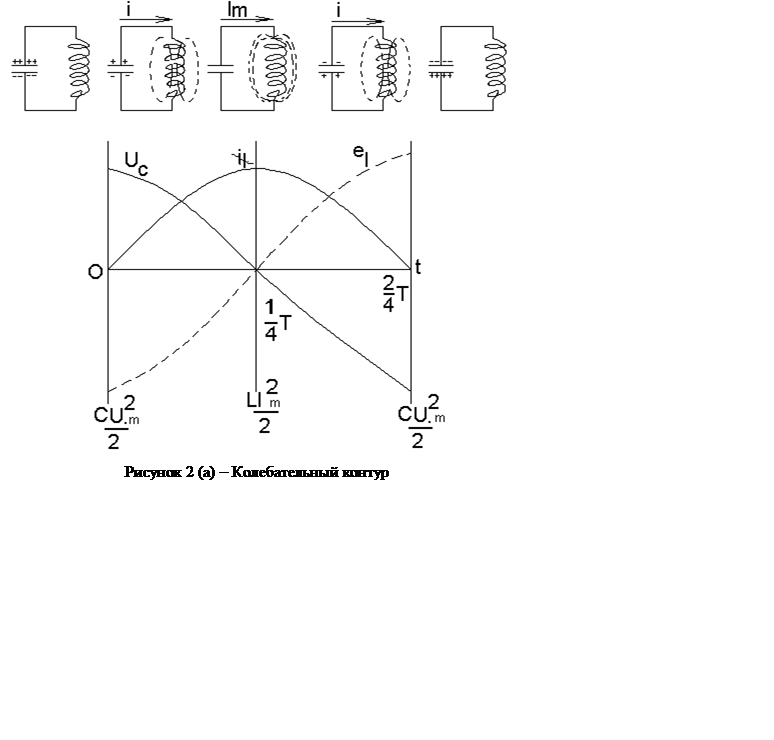
Итак, при разрядке конденсатора через катушку индуктивности в образовавшейся цепи возникают электрические колебания. В процессе этих колебаний происходит периодическое превращение энергии электрического поля в энергию магнитного поля и энергии магнитного поля в энергию электрического поля:
![]()
![]()
![]()
![]()
![]() Wэ Wм Wэ
Wм Wэ …
Wэ Wм Wэ
Wм Wэ …
Следует отметить, что, как и в случае механических колебаний, за один период колебаний происходит два цикла превращения энергии.
Полная энергия электрических колебаний в любой момент времени равна сумме энергий электрического и магнитного полей:
5 6 7 8 9
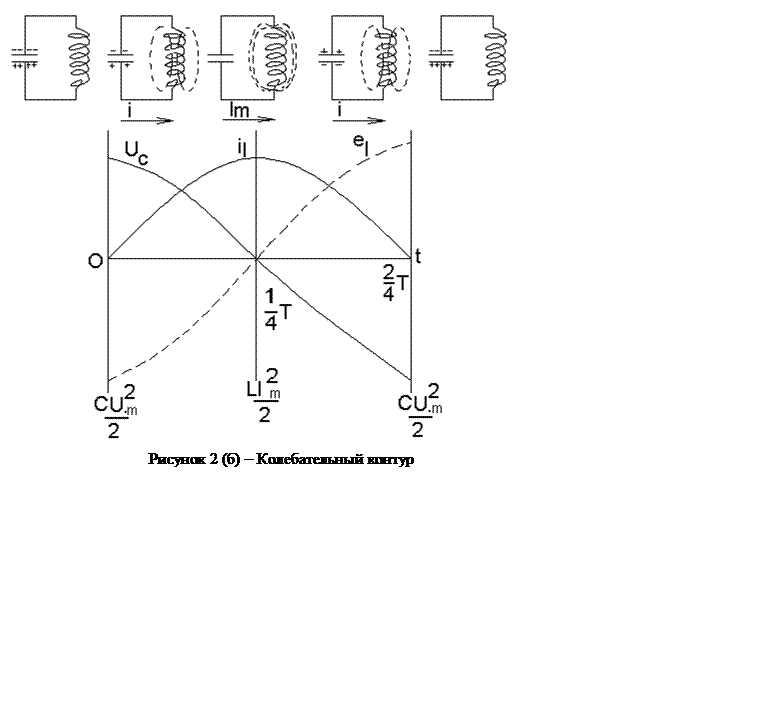 |
E = Wм + Wэ
По закону сохранения энергии полная энергия в идеальном контуре будет постоянной:
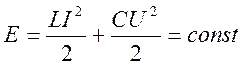
Её можно выразить через максимальные значения энергии электрического поля конденсатора или энергии магнитного поля катушки следующим образом:
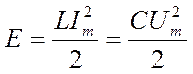
Отсюда:
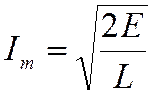 и
и 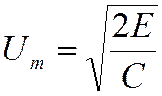
Это значит, что амплитуда свободных электрических колебаний (амплитуда колебаний силы тока и напряжения) прямо пропорциональна корню квадратному из энергии, сообщенной контуру в начальный момент, чтобы вывести эту колебательную систему из состояния равновесия, или, как принято говорить, амплитуда свободных колебаний зависит от интенсивности первоначального толчка.
3 Формула частоты и периода свободных колебаний в колебательном контуре. В предыдущем параграфе уже было отмечено, что суммарная энергия электрического поля конденсатора и магнитного поля катушки колебательного контура в любой момент равна максимальной энергии электрического поля конденсатора или максимальной энергии магнитного поля катушки:
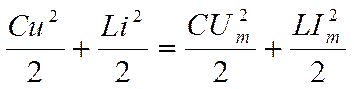
Подставляя сюда выражения для мгновенных значений напряжения u и силы тока i, получаем:
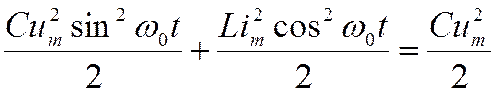
Преобразуем это равенство, учтя, что
Im = ω0qm = ω0CUm:
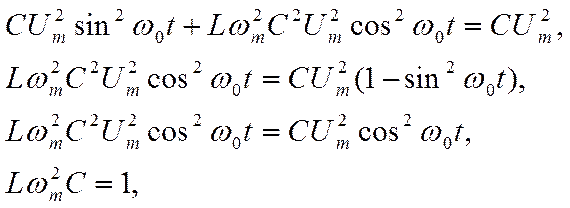
Следовательно:
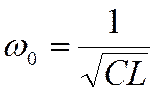
Это - формула Томсона для циклической частоты свободных электрических колебаний в колебательном контуре. Для частоты колебаний получаем формулу
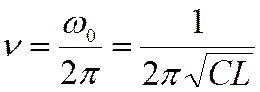
а для периода –
![]()
Чем меньше емкость конденсатора и индуктивность катушки, тем частота свободных колебаний выше, а период меньше.
Колебания в системах с трением
 Изучая свободные колебания, мы до сих пор не учитывали
сил трения (сопротивления) в колебательных системах. Такая идеализация
колебательных систем допустима потому, что во многих случаях трение (сопротивление)
столь мало, что им можно в ряде расчетов пренебречь. Так, потери энергии хорошим
камертоном за один период составляют 0,0001 его первоначальной энергии.
Идеализация колебательных систем позволяет значительно упростить рассмотрение
свободных колебаний.
Изучая свободные колебания, мы до сих пор не учитывали
сил трения (сопротивления) в колебательных системах. Такая идеализация
колебательных систем допустима потому, что во многих случаях трение (сопротивление)
столь мало, что им можно в ряде расчетов пренебречь. Так, потери энергии хорошим
камертоном за один период составляют 0,0001 его первоначальной энергии.
Идеализация колебательных систем позволяет значительно упростить рассмотрение
свободных колебаний.
Однако во всех реальных колебательных системах действуют силы трения (сопротивления).
 Запишем
график колебаний маятника с трением. Для этого прикрепим к маятнику фломастер
так, чтобы он касался равномерно движущейся бумажной ленты (рис. 3). Отведем
маятник в сторону и предоставим ему возможность колебаться. Включив двигатель,
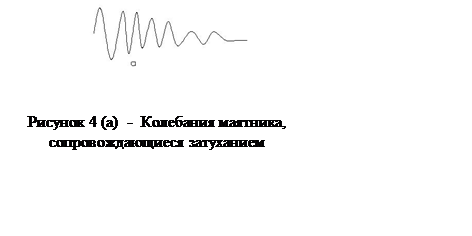
мы получим на движущейся бумажной ленте график колебаний маятника. Анализируя
этот график (рис. 4, а), мы видим, что размах колебаний маятника не остается
постоянным, а постепенно уменьшается. Колебания маятника затухают.
Запишем
график колебаний маятника с трением. Для этого прикрепим к маятнику фломастер
так, чтобы он касался равномерно движущейся бумажной ленты (рис. 3). Отведем
маятник в сторону и предоставим ему возможность колебаться. Включив двигатель,
мы получим на движущейся бумажной ленте график колебаний маятника. Анализируя
этот график (рис. 4, а), мы видим, что размах колебаний маятника не остается
постоянным, а постепенно уменьшается. Колебания маятника затухают.
Увеличим трение колеблющегося маятника (для чего
прижмем фломастер к бумаге) и повторим опыт. Анализ графика колебаний
показывает, что в этом случае затухание колебаний 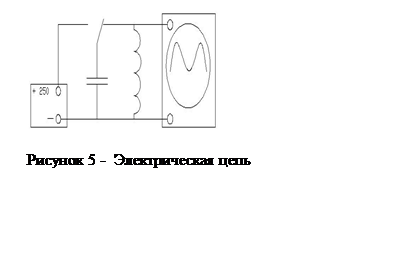 происходило
быстрее (рис. 4,б). Проделаем аналогичный опыт с электрическими колебаниями.
Соберем цепь изображенную на рисунке 5.
происходило
быстрее (рис. 4,б). Проделаем аналогичный опыт с электрическими колебаниями.
Соберем цепь изображенную на рисунке 5.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.