Гармонические колебания, уравнения, график, параметры. Электромагнитные свободные колебания. Автоколебания, страница 10

Таким образом, полная энергия гармонического колебания постоянна и пропорциональна квадрату амплитуды смещения. Это – одно из характерных свойств гармонических колебаний. Здесь постоянный коэффициент k в случае пружинного маятника означает жёсткость пружины, а для математического маятника k=mgH. В обоих случаях коэффициент k передаётся параметрами колебательной системы.

Полная энергия механической колебательной системы состоит из кинетической и потенциальной энергий и равна максимальному значению любой из этих двух составляющих:

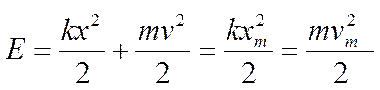
Следовательно, полная энергия колебаний прямо пропорциональна квадрату амплитуды смещения или квадрату амплитуды скорости.

Из формулы:

 

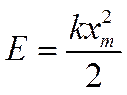
можно определить амплитуду x_m колебаний смещения:

 

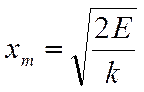Амплитуда смещения при свободных колебаниях прямо пропорциональна корню квадратному из энергии, сообщённой колебательной системе в начальный момент, когда систему выводили из состояния равновесия.

 Кинематика механических свободных колебаний

     1      Смещение, скорость, ускорение. Для нахождения кинематических характеристик (смещения, скорости и ускорения) свободных колебаний воспользуемся законом сохранения и превращения энергии, которой для идеальной механической колебательной системы записывается так:

 

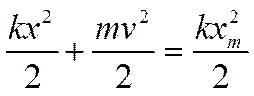или

 

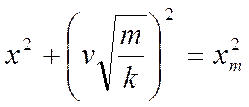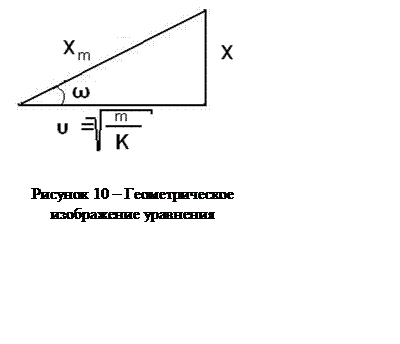
Полученное равенство можно представить геометрически в виде прямоугольного треугольника, у которого x_m – гипотенуза, а x и v - катеты ( рис. 10). Из рисунка видно, что

 

              

 

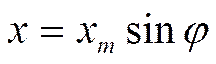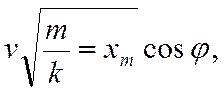
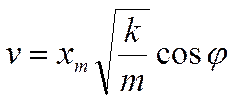          Из второго равенства находим выражение для мгновенной скорости, так как при колебании системы смещение x непрерывно изменяется, а амплитуда колебаний x_m является постоянной величиной, то непрерывно изменяется и угол. Выясним, как изменяется этот угол φ.

Для этого выразим скорость v как производную от смещения x по времени t:

υ= x^' = x_m cosφ · φ^'

Приравняв полученные два выражения для скорости, получим:

 

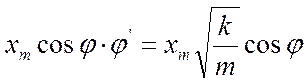или

 

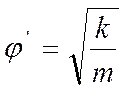Обозначим эту постоянную величину через ω₀:

 

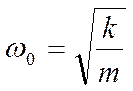Так как производная по времени φ^' постоянна, то угол φ зависит от времени линейно:

φ=ω₀t

Учитывая это можно записать:

x = x_m sin ω₀t, υ = x_m ω₀ cos ω₀t

Здесь величина

x_mω₀ = υ_m

есть амплитуда изменения скорости:

υ = υ_m cos ω₀t

Зависимость мгновенного значения ускорения a от времени t мы найдём как производную скорости υ по времени:

a = υ^' = - ω₀υ_m sin ω₀t,

или

a = -a_m sin ω₀t

знак «-» в полученной формуле указывает на то, что знак проекции вектора ускорения на ось, вдоль которой происходят колебания, противоположен знаку смещения x.

Итак, мы видим, что при гармонических колебаниях не только смещение, но и скорость и ускорение изменяются синусоидально.

     2 Циклическая частота колебаний.Величина ω₀ называется циклической частотой колебаний. Так как функция sin α имеет по аргументу α  период 2π, а гармонические колебания имеют по времени период T, то

ω₀T = 2π

Отсюда

 

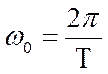или

 

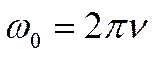
Так как частота υ выражает число колебаний за 1 с, то циклическая частота ω выражает число колебаний за 2π с.

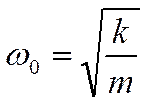     3      Формулы частоты и периода свободных колебаний для пружинного и математического маятников.Формула циклической частоты

непосредственно применима для вычисления циклической частоты свободных колебаний пружинного маятника (k -жёсткость пружин).

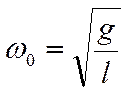Чтобы получить формулу циклической частоты свободных колебаний пружинного маятника, надо вместо k подставить l. Тогда получим:

Так как

 

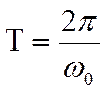то для периода свободных колебаний имеем:

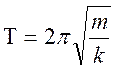- в случае пружинного маятника

и

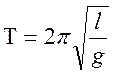          - в случае математического маятника.