Гармонические колебания, уравнения, график, параметры. Электромагнитные свободные колебания. Автоколебания, страница 7

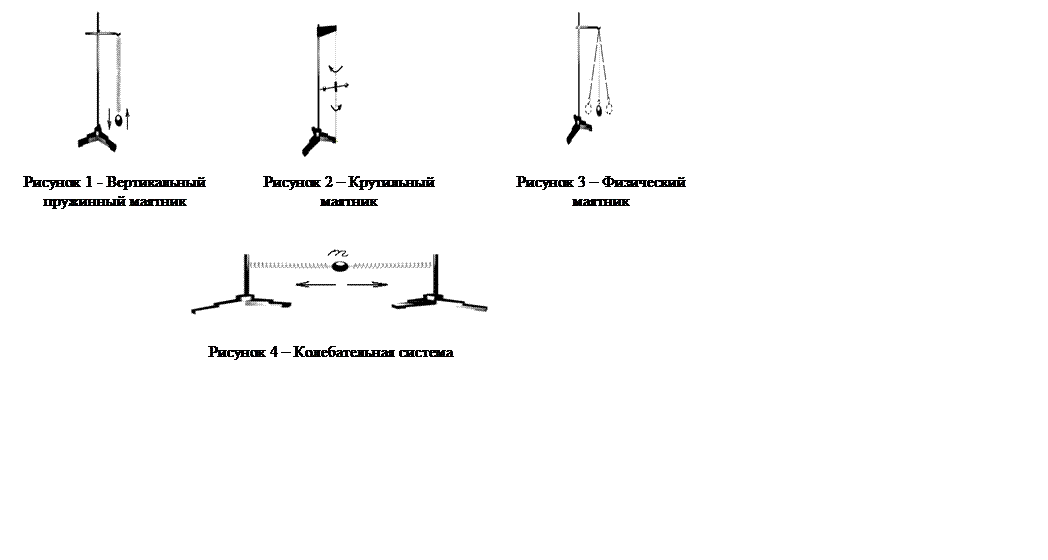
Земля, подставка и подвешенное к подставке тело (см. рис. 3) образуют колебательную систему, называемую физическим маятником. Стойки, две пружины и тело m (см. рис. 4) образуют колебательную систему, которую обычно называют горизонтальным пружинным маятником. Всем колебательным системам присущ ряд общих свойств. Рассмотрим главные из них.

     1 У каждой колебательной системы есть состояние устойчивого равновесия. У физического маятника – это положение, в котором центр массы подвешенного тела находится на одной вертикали с точкой подвеса. У  вертикального пружинного маятника – это положение, в котором сила тяжести уравновешивается силой упругости пружины. У горизонтального  пружинного маятника – это положение, при котором обе пружины деформированы одинаково.

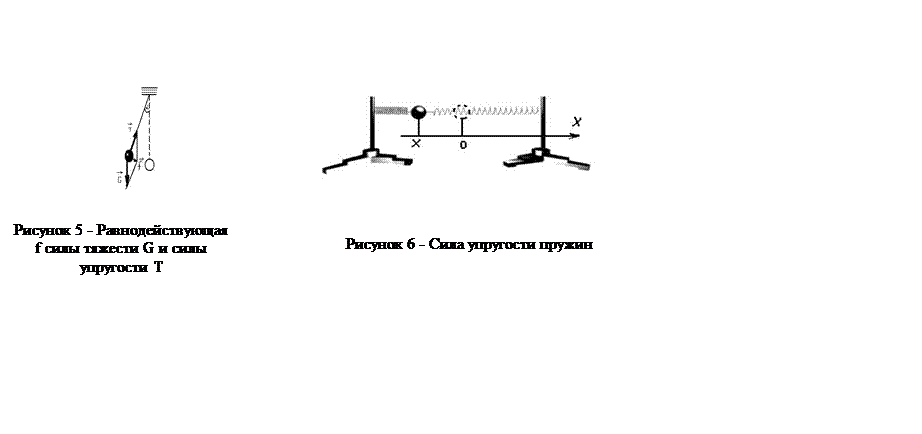
     2 После того как колебательная система выведена из положения устойчивого равновесия, появляется сила, возвращающая систему в устойчивое положение. Происхождение этой силы может быть различным. Так, у физического маятника – это равнодействующая f силы тяжести G и силы упругости T (рис.5), а у пружинных маятников – это сила упругости пружин (рис. 6).

     3 Возвратившись в устойчивое состояние, колебательная система не может сразу остановиться. В механических колебательных системах этому мешает инертность колеблющегося тела. Перечисленные свойства приводят к тому, что если колебательную систему тем или иным способом вывести из состояния устойчивого равновесия, то в ней в отсутствие внешних сил возникнут и некоторое время будут сохраняться колебания. Возникшие колебания могли бы продолжаться неограниченно долго, если бы в колебательной системе не было трения (сопротивления). Именно такие, идеальные колебательные системы мы во многих случаях будем рассматривать. Идеальная колебательная система имеет два определяющих признака:

     а) в ней отсутствует трение (сопротивление) и, следовательно, не происходит необратимых превращений энергии;

     б) параметры такой колебательной системы (длина нити, масса колеблющегося тела, жесткость пружины) постоянны.

Примером идеальной колебательной системы может служить так называемый математический маятник, представляющий собой груз малых размеров, подвешенный на гибкой невесомой и нерастяжимой пружине. Длина нити и масса груза в процессе колебания маятника остаются неизменными. Если нить считать бесконечно тонкой и идеально гибкой, а размеры груза бесконечно малыми, точечными, то при колебаниях математического маятника трения не будет.

В реальных колебательных системах имеется трение, а параметры системы в процессе колебательного движения немного изменяются. Так, маятник, представляющий собой груз конечных размеров, подвешенный на шелковой нити, нельзя считать в полном смысле идеальной колебательной системой, так как в процессе его колебательного движения действует сопротивление воздуха и трение в точке подвеса, а длина нити изменяется (хотя и совсем незначительно). Но при малых колебаниях такого маятника сопротивление воздуха мало, а длина нити меняется столь незначительно, что с известным приближением можно этот маятник считать почти идеальной колебательной системой. Это относится также к пружинному маятнику. Его можно считать идеальной колебательной системой, если масса колеблющегося тела и жесткость пружины постоянны, а трение столь мало, что его можно не учитывать.

1 Свободные колебания.Колебания, происходящие в колебательной системе, не подверженной действию периодических внешних сил, называются свободными колебаниями. Для возникновения свободных колебаний на колебательную систему должно быть оказано из вне кратковременное воздействие, выводящее систему из состояния равновесия (отклонение из среднего положения маятника, зажатой в тисках стальной линейки, струны и т.п.).

  2  Осциллограмма колебаний.Если грузом маятника будет служить сосуд с чернилами, в котором имеется узкое отверстие, то при колебаниях маятника: