Гармонические колебания, уравнения, график, параметры. Электромагнитные свободные колебания. Автоколебания, страница 3

Гармонические колебания. Уравнение и график гармонического колебания.

Параметры и мгновенные

характеристики. Закон сохранения энергии

Среди всевозможных движений большое распространение имеют колебания.

Колебания совершают электроны и молекулы, детали машин и сами  машины  и т.д.  Благодаря  колебаниям  мы слышим  и видим.   Наша  задача -  разобраться   в   природе   колебаний, выяснить их характерные особенности и свойства.

Нам известно, что причиной движения являются действующие на тело силы. Если,  к примеру, равнодействующая всех сил будет    равна нулю, то тело будет двигаться равномерно и прямолинейно; т.е. при

F_P = 0 => x =v×t

Если на тело будет действовать постоянная по величине - сила, направленная    одинаково    со    скоростью,    то    тело    будет двигаться равноускоренно, т.е. при

F = const   х= v₀t ± аt²/2

Допустим, что на тело действует сила, пропорциональная смещению, т.е. упругая сила, уравнение которой F. Используя второй закон Ньютона, найдём ускорение движения тела:

F = mа и F = - kx => а = - kx/m

Из механики известно, что ускорение есть вторая производная смещения x т.е.

а = d² x/ d t²

Итак, если вам известно уравнение смещения, то довольно просто найти ускорение. Но можно решить и обратную задачу, т.е. по ускорению /второй производной/ можно отыскать уравнение движения тела. Решая уравнение а = - kx/m относительно x можно найти, что

x = x₀ sin w t

Такое движение называется гармоническим колебанием, а материальную точку, совершающую такие колебания называют гармоническим осциллятором.

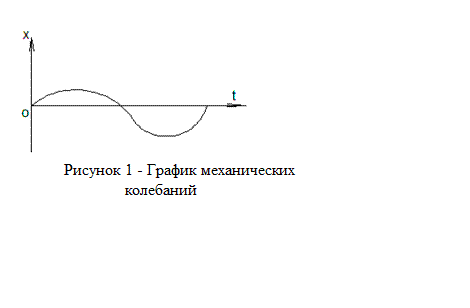
Графиком гармонического колебания будет синусоида     (рисунок 1). Можно утверждать и обратное: если материальная точка движется по закону

x = x₀ sin w t,

то она совершает гармонические колебания и на нее должна действовать сила типа

F = -k x

 Время одного колебания тела называют периодом колебания Т. Период измеряется в секундах. Величину, обратную периоду, называют     частотой колебания = 1/T. Единицей частоты служит Герц (Гц).

При Т = 1 с.

v = 1 1/с = 1 Гц.

Частота показывает число колебаний за одну секунду.

Величину

w = 2pu = 2 p/Т

называют круговой частотой, а ее единицей будет

                                        1 рад/с = 1 1/с

Обычно x₀ (А) называют амплитудой колебания. Она равна максимальному смещению при колебаниях и измеряется метрами.

Кроме постоянных параметров для колебания можно ввести мгновенные характеристики.

x = x₀sinwt - смещение материальной точки;

                    V = x¹ = wc₀coswt - скорость движения;

                           a = x¹¹ = -w²c₀sinwt -ускорение;

                    F = -kx - возвращающая сила;

                                       φ=  wt - фаза колебания или фазовый угол

Если при t = 0 х ¹ 0, то фазовый угол будет j = j₀ где j₀ - начальная фаза. При колебаниях материальной точки потенциальная энергия превращается в кинетическую и наоборот. Если система изолированная, то энергия сохраняется, то есть полная энергия остается без изменения

Wo = W_k + W_n = const

Для гармонического осциллятора полная энергия:

W0 = mw²x₀²/2

Свободные колебания

Колебательная система совершает свободные колебания, если её вывести из состояния равновесия. Ознакомимся с механическими
свободными колебаниями на примерах пружинного и математического маятников и электромагнитными свободными колебаниями, источниками которых будут колебательный контур и атом.

Механические свободные колебания. Колебания пружинного маятника

Пружинный маятник представляет собой груз массой m креплённой  на  пружине,  коэффициент   упругости  которой  К. Запись     колебания на экране осциллографа  показывает, что свободные  колебания  пружинного  маятника  затухают   из-за трения (рисунок 3). Отклонения груза от положения равновесия со временем убывают. Свободные колебания нельзя считать гармоническими в полном смысле слова. Если сила трения мала, то затухание небольшое и колебания пружинного маятника можно считать гармоническими. Опыт показывает, что трение влияет на убыль амплитуды, период остаётся постоянным.