 |
3 Гармонические колебания.Наблюдая за свободными
колебаниями маятника, можно заметить, что: а) максимальное отклонение колеблющегося тела вправо от положения равновесия равно его максимальному отклонению влево; б) время отклонения вправо равно времени отклонения влево; в) характер движения тела вправо и влево от положения равновесия одинаков, а внимательное рассмотрение осциллограммы этих колебаний позволяет высказать предположение, что она представляет собой синусоиду. В дальнейшем мы убедимся в том, что в случае идеальной колебательной системы осциллограмма колебаний действительно является синусоидой. Такие колебания, длящиеся неограниченно долго, называют гармоническими. Правильные синусоидальные, т.е. гармонические, свободные колебания могут происходить только в идеальной колебательной системе. В реальных колебательных системах из-за трения имеют место необратимые преобразования энергии, и осциллограмма свободных колебаний в большей или меньшей мере отличается от синусоиды.
4 Величины, характеризующие гармонические колебания. Для описания гармонических колебаний, кроме скорости и ускорения, введены новые специфические для этого вида движения величины. Одной из таких величин является смещение. В случае прямолинейного колебательного движения смещением называется проекция перемещения колеблющегося тела от его равновесного положения на ось, параллельную прямой, вдоль которой происходит движение тел.
При колебательном движении мгновенные значения смещения х скорости ν и ускорения а непрерывно изменяются.
Но для характеристики гармонического, колебательного движения важны максимальные значения смещения, скорости и ускорения, которые называются амплитудными значениями или амплитудами:
x m, υ m и a m
Значение величин, характеризующих гармонические колебания, повторяются через равные промежутки времени Т, называемые периодом колебаний. Если за время t произошло колебаний N, то период колебаний определяется формулой
![]()
|
Таким образом, периодом гармонического колебания называется время, за которое совершается одно полное колебание. Число колебаний, совершаемых телом в 1 с, называется частотой колебаний.. Частоту колебаний обычно обозначают буквой υ. Если за время t совершается N полных колебаний, то
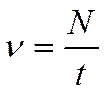
Частота показывает, сколько полных колебаний совершается в 1 с. За единицу частоты принимается частота, при которой в 1 с совершается одно колебание. Эта единица частоты называется герц (1 Гц). Название единице частоты дано в честь известного немецкого физика Генриха Герца. На практике для измерения частоты пользуются кратными единицами: килогерц, мегагерц и гигагерц. Сравнение формул для периода и частоты показывает, что период и частота – величины взаимно обратные:
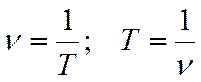
Динамика и энергетика механических свободных колебаний
1 Динамика. Рассмотрим динамику колебаний пружинного и математического маятников.
Отведём шар пружинного маятника от положения равновесия на небольшое расстояние, при котором деформация пружин будет упругой (см. рис. 6). В этом случае на шар будет действовать возвращающая сила, направленная в сторону положения равновесия. Эта сила (по закону Гука) пропорциональна смещению тела от положения равновесия:
F = - kx
Здесь знак «минус» указывает на то, что возвращающая сила ƒ направлена к положению равновесия, а её проекция всегда имеет знак, противоположный знаку смещения х. Аналогично обстоит дело в случае математического маятника. Отведём математический маятник на небольшое расстояние от положения равновесия (см. рис. 5). В этом случае равнодействующая силы тяжести и силы упругости нити направлена в сторону положения равновесия. Эту силу можно выразить так:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.