Гармонические колебания, уравнения, график, параметры. Электромагнитные свободные колебания. Автоколебания, страница 12

ЧО₂ Электромагнитные свободные колебания

 Колебательный контур

Электромагнитные свободные колебания

     До сих пор мы рассматривали колебания, которые возникают в идеализированных механических колебательных системах. Однако колебания могут иметь и электромагнитную природу.

   1    Колебательный контур.Зарядив конденсатор от источника постоянного тока, замкнем заряженный конденсатор на катушку индуктивности, параллельно которой подключен электронный осциллограф (рис.1). На экране осциллографа мы увидим осциллограмму, которая свидетельствует о том, что в образовавшейся цепи появились электрические колебания.

Следовательно, цепь, состоящая из конденсатора и катушки индуктивности, является колебательной системой. Такая цепь получила название колебательного контура. Внимательное рассмотрение осциллограммы убеждает в том, что свободные колебания в колебательном контуре являются синусоидальными, т.е. гармоническими. При этих колебаниях синусоидально изменяются сила тока в контуре, заряд и напряжение на обкладках конденсатора. Однако по фазе колебания заряд и силы тока не совпадают. Действительно, предположим, что начало отсчета времени, выбрано так, что начальная фаза изменения заряда равна нулю, т.е.

q = q_msinω₀t

где q _m – максимальный заряд на обкладках, ω₀  - циклическая частота колебаний. Но сила тока i выражает изменение заряда на обкладках за 1 с, т.е. представляет собой скорость изменение заряда. Поэтому силу тока можно найти как производную от заряда

i = q′ = ω₀cosω₀t = I_m cosω₀t

где I_m = ω₀q_m есть амплитудное значение силы тока. Это значит, что изменение силы тока сдвинуто по фазе относительно изменения заряда на , или по времени на четверть периода. Напряжение на контуре связано с зарядом конденсатора соотношением

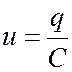
Поэтому изменение напряжения происходит синфазно с изменением заряда:

u = U_msinω₀t

    2   Преобразование энергии в колебательном контуре.

Допустим, что мы имеем колебательный контур, в котором:

а)  отсутствует сопротивление проводников, а следовательно, и не происходит необратимых преобразований энергии;

б) емкость конденсатора и индуктивность катушки остаются неизменными. При подключении конденсатора к источнику постоянного напряжения в нем накапливается определенное количество электрической энергии:

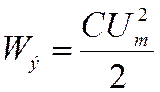
          Этой энергией обладает электрическое поле конденсатора.

После присоединения конденсатора к катушке индуктивности в ней возникает электрический ток и связанное с этим током магнитное поле. При возникновении магнитного поля, т.е. при нарастании его индукции, в катушке возникает индуцированное электрическое поле, которое по закону Ленца противодействует нарастанию силы тока. Из-за этого сила тока в контуре нарастает не скачком, а постепенно.

Прохождение тока по катушке связано с постепенной разрядкой конденсатора. Наконец, наступит такой момент, когда конденсатор окажется полностью разряженным, а сила тока достигнет максимального значения. К этому моменту энергия электрического поля конденсатора окажется полностью превращенной в энергию магнитного поля катушки:

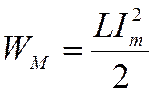
В следующее мгновение сила тока и индукция связанного с ним магнитного поля начинают убывать. Это снова приводит к появлению индуцированного электрического поля, которое в этом случае будет противодействовать убыванию силы тока в катушке. Однако в контуре начинается перезарядка конденсатора и нарастание разности потенциалов на обкладках конденсатора является причиной уменьшения силы тока в цепи. Когда сила тока станет равной нулю, перезарядка конденсатора закончится. К этому моменту энергия магнитного поля целиком преобразуется в энергию электрического поля (рисунок 2  (а), 1-5).

В дальнейшем процесс повторится с той только разницей, что изменятся направления тока, линий напряженности электрического поля в конденсаторе и линий индукции магнитного поля катушки (рисунок 2 (б), 5-9).