Физика \ Физика

Гармонические колебания, уравнения, график, параметры. Электромагнитные свободные колебания. Автоколебания, страница 4


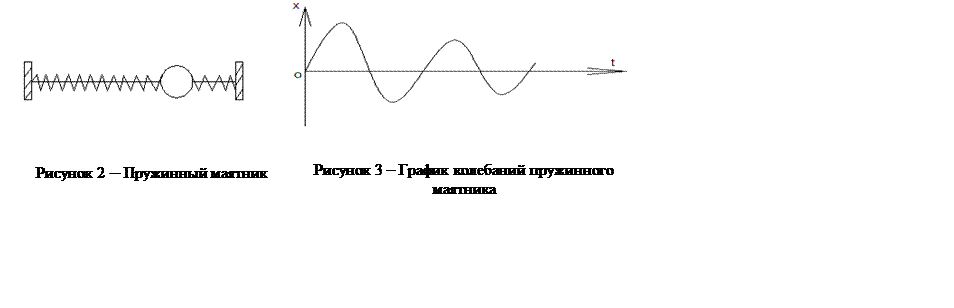
 Найдём     период    свободных    колебаний     пружинного маятника из следующих соображений: F = -kx в тоже время:

F = ma = -mw2x Þ  -mw2x = -kx

Значит

w=

Учитывая, что

w = ,

получаем

=,

откуда

Т = 2p

Таким образом, период колебания зависит только от массы маятника и коэффициента упругости пружины.

Колебания математического маятника

Математический маятник представляет собой материальную точку, укреплённую на невесомой и нерастяжимой нити. Практически это тяжелый шарик, подвешенный к длинной и прочной нити, масса которой значительно меньше массы шарика (рис. 4), При небольших углах отклонения можно считать колебания математического маятника гармоническими. На самом деле, если  очень мал, то DАОВ и BCD можно считать подобными. Из подобия треугольников находим, что 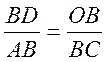     , т.е.           

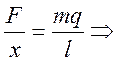   F =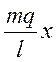

Нетрудно заметить, что при положительном смещении х сила F отрицательна и наоборот, а это значит                                 

 F=-mq/ l

Так как нить нерастяжима, то

    mg / 1  = k

при колебаниях остаётся постоянной, следовательно- F=-kх, а это позволяет утверждать, что колебания маятника будут гармоническими.

Вычислим период колебания математического маятника: сравнивая силы    F = - mw2х и   F = xmq/l  находим, что

w = ,

Заменим w = 2p/T и окончательно находим период колебания

                                                T = 2p

Период колебания математического маятника зависит только от длины маятника и ускорения свободного падения. От массы и амплитуды период колебания не зависит.

Электромагнитные свободные колебания.

Колебательный контур

Электрическая цепь, состоящая из катушки с индуктивностью L, конденсатора с емкостью С и резистора с сопротивлением R, называется колебательным контуром. Если    замкнуть    на    короткое    время    ключ,    зарядить конденсатор /рис. 5/ и предоставить контур самому себе,   то в контуре возникнут свободные электромагнитные колебания.

Энергия, запасенная контуром, постепенно расходуется на нагрев и на излучение в виде электромагнитного поля, поэ­тому колебания в контуре быстро затухают /рис. 6/. Период свободных колебаний определяется индуктивностью и емкостью контура

T=2p

 


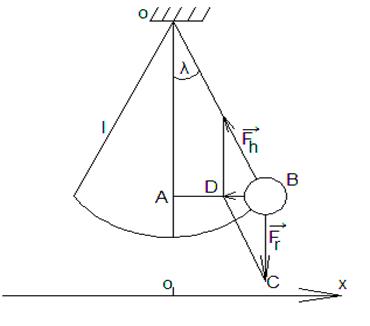Рисунок 4 -  Математический маятник

Энергия электрического поля при разрядке конденсатора превратится в энергию магнитного поля катушки. Магнитное поле, исчезая, создает ток в цепи, и конденсатор перезарядится, т.е. энергия магнитного поля катушки превратится в энергию электрического поля конденсатора. Потом процессы повторятся, таким образом, в колебательном контуре электрическое и магнитное поля будут периодически изменяться. Такие изменения электромагнитного поля называют электромагнитными.

Атом как источник электромагнитных колебаний

Атомы при определенных условиях становятся источниками электромагнитных колебаний. Теория излучения и поглощения энергии атомами была разработана в 1913 г. датским физиком Н. Бором. Идеи Бора получили свое дальнейшее развитие в современной физике. Познакомимся с основными положениями этой теории.

Как мы знаем, атом состоит  из  положительно заряженного    ядра, вокруг которого  движутся электроны. Для   простоты   будем   рассматривать простейший атом, атом водорода. По идее Бора для    атома   должны  соблюдаться следующие положения:

1 Каждый электрон кроме основной орбиты, имеет ряд запасных, так называемых дополнительных орбит, (рис. 7). Электрон может двигаться только по одной из дополнительных орбит. Атом  при  этом  будет иметь строго определённый  уровень энергии.

              2 Когда электрон движется по дозволенной орбите, атом находится   в   устойчивом  состоянии,  т.е.   не   излучает и не поглощает энергию.

             3 Излучение и поглощение энергии атом производит тогда, когда электрон переходит «перескакивает» с одной орбиты на другую. По мере удаления электрона от ядра, атом поглощает энергию, а при переходе на более близкие орбиты излучает. И в этом и в другом случае энергия атома изменяется порциями или квантами. Энергия кванта находится так

Скачать файл