Амплитуда любой гармоники:
![]() ,
, ![]() ,
,
![]() , …
, …
Таким образом, разложение заданной функции имеет вид:
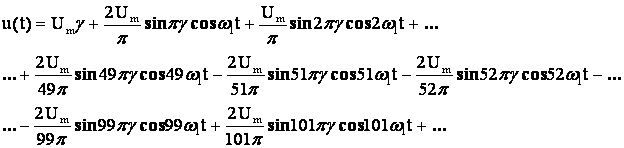
Положительные знаки перед членами ряда указывают на то, что начальная фаза гармоники равна +90°, отрицательный знак – начальная фаза гармоники -90°. Таким образом, каждый раз при переходе амплитуды гармоники через нуль ее начальная фаза меняется на 180°. Часто спектральную диаграмму изображают только над осью абсцисс, имея по-прежнему в виду, что начальные фазы гармоник, расположенные по разные стороны от частот f0k сдвинуты на 180°.
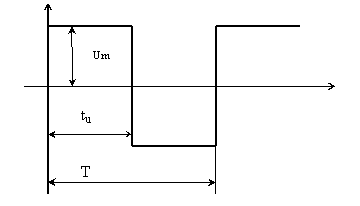
Рис. 2.
Пример 2. Разложить в ряд Фурье прямоугольный периодический сигнал представленный на рис. 2 со скважностью q = 2.
Решение. Имеем симметрию относительно оси абсцисс и начала координат. Поэтому спектр содержит только синусоидальные составляющие.
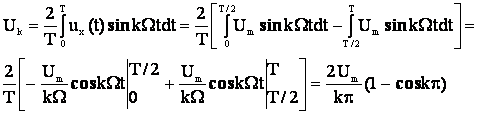
Таким образом, спектр содержит бесконечное количество нечетных синусоидальных гармоник, амплитуда которых обратно пропорционально номеру гармоники – с его увеличением они уменьшаются по гиперболическому закону. Несмотря на то, что спектр импульса бесконечен, можно наметить верхнюю границу спектра (ограничить спектр). Для прямоугольных импульсов 95% сей энергии сигнала сосредотачивается в диапазоне частот до f = 2/tu.
Пример 3. Разложить в ряд Фурье прямоугольный периодический сигнал представленный на рис. 1 со скважностью q = 2.
Решение. Имеем симметрию относительно оси ординат, значит, спектр содержит постоянную составляющую и косинусоидальные составляющие.
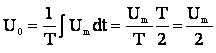
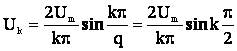
![]()
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.