Лекция № 3, модуляция, формы описания сигналов и их спектры, страница 3

         2. Спектральная форма. Многие задачи анализа и синтеза реальных сигналов упрощаются благодаря тому, что эти сигналы, как правило, сложные по форме, можно представить  идее комбинации простых сигналов. Для этого сложный сигнал представляют в идее спектра (преобразование Фурье).

         3. Векторная форма. Каждая гармоника изображается в виде вектора.

Спектры сигналов.

         Важнейшей характеристикой сигнала являются его частотные свойства (проблема согласования частотных характеристик сигнал и КС). Главное внимание при рассмотрении сигналов уделяется определению ширины их спектра (основной фактор при согласовании сигнала с КС – для исключения потери информации ширина спектра не должна превышать полосы пропускания КС). Если ширина спектра сигнала бесконечна, зная спектральный состав (энергию каждой гармоники), можно выделить эффективную ширину спектра,  которой сосредоточена основная энергия сигнала.

         По виду спектры можно разделить на:

·  дискретные спектры периодических сигналов. Отдельные гармоники отстоят на одинаковое расстояние друг от друга;

·  непрерывные спектры. Расстояние между гармониками равно нулю;

·  дискретные спектры непериодических сигналов. Расстояние между отдельными гармониками непостоянно.

Любой реальный сигнал удовлетворяет условиям Дирихле и поэтому может быть разложен на гармоники. Для периодического сигнала  u_x(t) с периодом Т спектр определяется как:

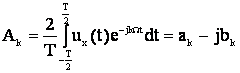                         ,                       (1)

где

;

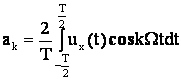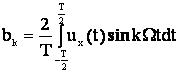;                                                                               (2)

 - модуль величины А_k;

 - фаза k-ой гармоники;

Т – период сигнала;

 - основная круговая частота.