Лекция № 3, модуляция, формы описания сигналов и их спектры, страница 5

·  Если кривая симметрична относительно начала координат, то в разложении отсутствуют косинусоидальные гармоники и постоянная составляющая.

·  Если кривая симметрична относительно оси абсцисс, то в разложении отсутствуют постоянная составляющая и гармоники четных номеров.

Совокупность гармоник, составляющих данное несинусоидальное колебание, представляет собой спектр этого колебания. Графическое изображение спектра называют спектральной диаграммой.

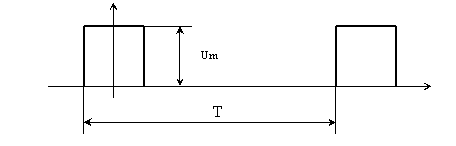
Рис. 1.

         Пример 1. Разложить в ряд Фурье прямоугольный периодический сигнал с Т = 1мс, t_u = 20 мкс.

         Решение. Сигнал симметричен относительно оси ординат – поэтому спектр не содержит синусоидальные составляющие, т.е.

,

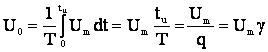где q = T/t_u – скважность,  g = t_u /Т – коэффициент заполнения.

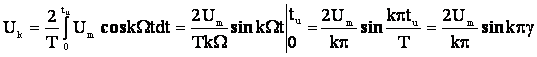                (4)

при , где n=1, 2, …, множитель . Номер гармоник k₀₁, k₀₂, …, k_0n выпавших из разложения определяется из выражения:

.

         В нашем случае q = T/t_u =50, значит k₀₁=50, k₀₂=100, k₀₃=150 и т.д., а частота этих гармоник f_0n= k_0n f₁=nq/T=n/ t_u: f₀₁=50 кГц, f₀₂=100 кГц, f₀₃=150 кГц и т.д. Выражение (4) можно записать в виде:

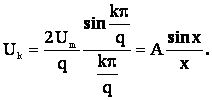
         Таким образом, спектр представляет собой гармоники, амплитуда которых вписывается в затухающую по закону 1/x косинусоиду. Легко убедиться, что при  f < f₀₁, sin kpg > 0  при f₀₁ < f< f₀₂, sin kpg < 0 и т.д. Часто спектральную диаграмму чертят только над осью абсцисс имея ввиду, что начальные фазы гармоник по обе стороны от f_0n сдвинуты на 180°.