Лекция № 3, модуляция, формы описания сигналов и их спектры, страница 10

.

         В случае, если информационный сигнал представляет собой обыкновенную синусоиду, то модулирующую функцию можно записать:

,

         где  - максимальное отклонение  частоты от  или девиация частоты. Поскольку ,  то  .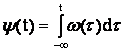

После ряда преобразований получаем:

,                                                (1)

         где  - называется индексом модуляции. В случае более сложной модулирующей функции, представляющей набор из n гармоник, ЧМ – сигнал будет описываться выражением:

         .

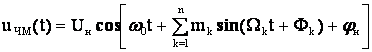Где  - частичные индексы модуляции.

         Если модулируемая функция достаточно гладкая, то внешне осциллограммы ФМ –  и ЧМ – сигналов не отличаются. Однако имеется принципиальная разница: фазовый сдвиг между ФМ – сигналом и немодулированным колебанием пропорционален исходному сообщению, в то время как для ЧМ – сигнала этот сдвиг пропорционален интегралу от передаваемого сообщения. При ЧМ девиация частоты пропорциональна амплитуде низкочастотного сигнала. В то же время величина  не зависит от частоты модулирующего сигнала. В случае ФМ ее индекс m оказывается пропорционален амплитуде низкочастотного сигнала независимо от его частоты, а значит, что девиация частоты при ФМ линейно увеличивается с ростом частоты. 

Спектральное разложение угловой модуляции.

         Запишем выражение (1) в виде:

и разложим его по правилу косинуса суммы:

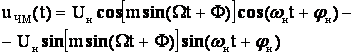                                          (2)

При индексе модуляции , в приближении можно записать: