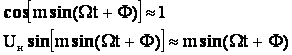Лекция № 3, модуляция, формы описания сигналов и их спектры, страница 11

.

Учитывая это выражение (2) приобретает вид:

.

Раскладывая произведение синусов  в конечной форме получаем спектр для ЧМ – сигнала с модулирующей функцией в виде одной гармоники с индексом модуляции много меньше единицы:

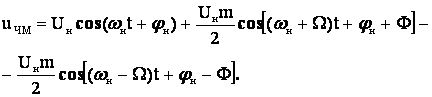
         Таким образом, при вышеизложенном случае спектр ЧМ – сигнала совпадает со спектром АМ – сигнала. Анализ более общего случая, когда m сравнима с единицей и больше нее показывает, что спектр и имеет неограниченный спектр. Однако амплитуды гармоник с номерами начиная с m+1 и далее быстро убывают и стремятся к нулю. Поэтому спектр ЧМ – сигнала с любым индексом модуляции m можно считать равным:

.

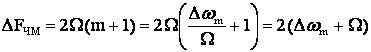В случае сложной модулирующей функции  является наивысшей гармоникой модулирующей функции.

         В случае частотной манипуляции, когда передаются дискретные сигналы 1 и 0 на двух им соответствующих частотах, сигнал на выходе модулятора можно рассматривать как суперпозиция двух сигналов с амплитудной манипуляцией, один из которых имеет несущую ¦₁, а другой ¦₂. Соответственно спектр частотной манипуляции может быть представлен как суперпозиция спектров двух АМ – сигналов. Если спектр видеоимпульса , а следовательно радиоимпульса, т.е. АМ, , то:

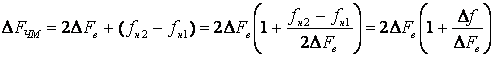
где - девиация частоты. Отношение девиации частоты к скорости телеграфирования (скорости модуляции) называется скоростью:

m_ЧМ = D¦/В.                       

Получение сигналов с угловой модуляцией.

         Структурная схема модулятора Амстронга изображена на рисунке. Немодулированной составляющей    отвечает  постоянный  вектор

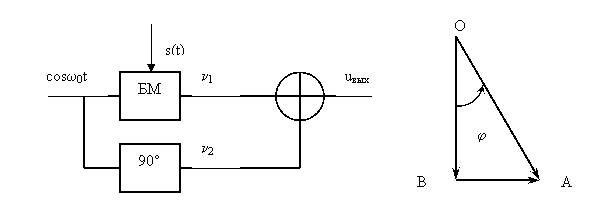
OB длиной . Балансно-модулированный сигнал  отображается вектором ВА. Длина этого вектора  непостоянна во времени, однако он всегда перпендикулярен вектору ОВ. Результирующий вектор ОА с течением времени будет поворачиваться, имея центр вращения в точке О. Обычно стремятся получить линейную зависимость между сигналом s(t)  и фазовым углом j(t). Для этого устанавливают такой режим работы модулятора, когда , так что . Модулятор Амстронга должен работать с малым индексом модуляции, т.е. с малой девиацией частоты. Чтобы преодолеть этот недостаток, в передатчиках ФМ- и ЧМ-сигналов после модулятора предусматривают многократное умножение частоты. Если на входе умножителя девиация частоты составляет Dw, то на выходе она будет равна nDw, где n – кратность умножения.