Элементы расчета и конструирования гиперболоидного масс-спектрометра типа «Фильтр масс»: Учебное пособие к курсовому проектированию, страница 7

а для масс, больших М_гр  равно:

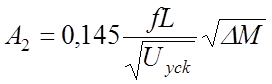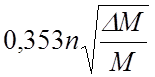                                =.                                  (60)

Из выражения (60) следует, что время пролета ионом анализатора, необходимое для того, чтобы на массе М обеспечивалась разрешающая способность  по уровню 100/А₂  (%), выраженное в числе периодов ВЧ колебаний электрического поля анализатора, имеет значение:

                                       ,                                                   (61)

что согласуется по характеру зависимости с аналогичным выражением из работы [8], т.е. при упомянутых выше условиях обеспечения разрешения по 50%-ному уровню (А₂=2) время пролета ионом анализатора должно быть равно , а для разрешения по 10%-ному уровню (А₂=10) .

Расчет показывает, что условие (60) достаточно жесткое, поскольку начальная энергия поступательного движения иона вдоль оси z, удовлетворяющая этому соотношению при А₂=10,  и обычных параметрах анализатора (L=20см, f=3МГц) достаточно мала (eU_yck=2,36 эВ).

   6. Определение скорости регистрации спектра масс

Под скоростью регистрации будем понимать скорость сканирования по спектру масс. Из выражения (15) для коэффициентов q и a, входящих в уравнения Матье (12) и (13),

                                                                    

или, что то же,

                                   ,                                    (62)

где V и U – напряжения, в; r₀– радиус поля, см, можно заключить, что последовательная во времени развертка спектра масс теоретически можно осуществляется изменением: 1) напряжений V и U (при сохранении неизменной величины ; 2) частоты электрического поля анализатора fи 3) радиуса поля анализатора (r₀), что, по-видимому, нельзя реализовать разумным образом в какой-либо конструкции. В первом случае для осуществления линейной во времени развертки напряжения V и U  необходимо изменять по так называемому пилообразному напряжению с линейной зависимостью V (и U) от времени V =b_vt, тогда как во втором случае для осуществления линейной по массам развертки частоту f  необходимо изменять по обратному квадратичному закону, делая ее следующей функцией от времени .

Учитывая данное выше определение скорости регистрации, можно после дифференцирования выражения (62) по времени получить формулу для расчета скорости регистрации спектров масс КМ:

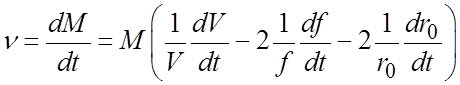                        .                                (63)

Ясно, что при развертке спектра первым из указанных способов частота f  и радиус r₀ постоянны во времени, поэтому выражение (62) упрощается:

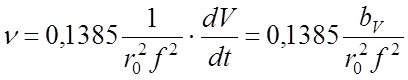          при V=b_Vt  и  b_V=const .               (64)

То же можно сказать и о развертке по второму способу (изменением частоты f):

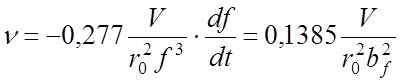                      при 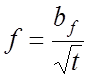 и b_f=const,                (65)

b_V и  b_f – коэффициенты пропорциональности, в/с и  МГц·с^1/2 соответственно; - скорость регистрации, а.е.м./сек. Варьируя значения входящих в формулы (64) и (65) величин, можно осуществлять изменение скорости регистрации  в весьма широких пределах. При этом важно оценить, в какой мере изменение влияет на основные параметры КМ.

Одно из очевидных влияний изменения  на чувствительность и разрешающую способность обусловлено тем, что с изменением  пропорционально изменяется ширина энергетического спектра масс, представляющего собой последовательность электрических импульсов, длительность которых равна 1/ . При условии неискаженного, оптимального с точки зрения шумовых характеристик усиления сигнала  изменение  влечет за собой изменение полосы пропускания усилителя и уровня шумового сигнала на выходе регистрирующего устройства, определяющего чувствительность КМ. Это чисто радиотехническое явление, а здесь же рассмотрим случаи изменений , при которых могут нарушаться процессы анализа ионов по их массам, когда движение ионов в анализаторе перестает подчиняться уравнениям Матье (12) и (13).

Строго говоря, движение ионов в анализаторе соответствует указанным уравнениям лишь при работе КМ в статическом режиме, когда прибор настроен на ионы одной определенной массы и нет развертки спектра масс, т.е. коэффициенты а и q в уравнениях Матье постоянны (случай =0). При осуществлении последовательной во времени развертки спектра масс за время пролета ионом анализатора (t_L) значения коэффициентов а и q не остаются постоянными. Если скорость  сравнительно невелика, изменениями а и q можно пренебречь. Однако  делать это можно лишь до тех пор, пока время пролета ионом анализатора много меньше времени анализа одной массы (т.е. длительности импульса спектра масс, равной 1/). При соизмеримости этих величин ион, будучи стабильным при влете в анализатор, окажется нестабильным при подлете его к концу, и решение вопроса – пройдет ли он анализатор или осядет на его полеобразующие электроды – становится неопределенным, так как в этом случае движение иона в анализаторе будет подчиняться другим более сложным уравнениям, чем уравнения Матье (12) и (13).

В работе [1] приводится соотношение, определяющее максимальную скорость регистрации фильтра масс и связывающее возможную скорость регистрации спектра масс в  диапазоне масс М (при условии разрешения пика на уровне 1/А_2н от его амплитуды) с основными параметрами анализатора (f, L, U_уск), а также с величиной предельно допустимого уменьшения интенсивности тока стабильных ионов (h)

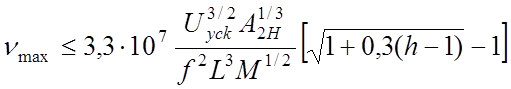                      .                          (66)   

Таким образом, в КМ, работающем в диапазоне массы 50 а.е.м. при частоте ВЧ-электрического поля, равной 2 МГц, длине анализатора 20 см, ускоряющем ионы напряжении 50 в, разрешении на 5% уровне (А_2н=20) и допустимом уменьшении интенсивности пика данной массы в 3 раза, максимальная скорость регистрации будет равна 37000 а.е.м./сек. Это вполне сравнимо со скоростями регистрации в самых быстродействующих времяпролетных масс-спектрометрах.   

Выражение (66) дает основание для суждения о том, как влияет скорость регистрации на величину достижимой абсолютной разрешающей способности. Исключая из (3.5) U_уск и L можно получить:

                .               (67)