Найдем аналитическое выражение стабильной траектории.
Точкам, выбранным на диаграмме (a, q) области стабильности (см. рис. 4), соответствуют чисто
мнимые дробные значения показателя степени ![]() в
решении канонического уравнения Матье (17):
в
решении канонического уравнения Матье (17):
![]() , 0<
, 0<![]() <1.
(20)
<1.
(20)
Выражение (17) с учетом (20) можно преобразовать к виду
![]() (21)
где
(21)
где ![]() и
и ![]() -
четная и нечетная функции Матье действительного дробного порядка
-
четная и нечетная функции Матье действительного дробного порядка ![]() [15]. Разложение этих функций в ряд по
тригонометрическим функциям имеет вид:
[15]. Разложение этих функций в ряд по
тригонометрическим функциям имеет вид:
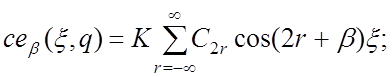 (22)
(22)
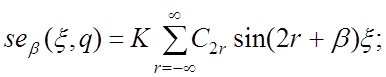 (23)
где С0=1, а К – нормирующий множитель [15].
Из общего решения (21) для канонического уравнения Матье (16) можно найти общие
решения для уравнений (12) и (13):
(23)
где С0=1, а К – нормирующий множитель [15].
Из общего решения (21) для канонического уравнения Матье (16) можно найти общие
решения для уравнений (12) и (13):
![]() (24)
(24)
![]() (25)
(25)
где 0<![]() <1;
0<
<1;
0<![]() <1; A, B, C, D –
постоянные интегрирования. Соотношения (24) и (25) представляют собой
аналитическое выражение траектории стабильного иона в параметрической форме.
Постоянные интегрирования находятся по известным начальным условиям,
обозначаемым
<1; A, B, C, D –
постоянные интегрирования. Соотношения (24) и (25) представляют собой
аналитическое выражение траектории стабильного иона в параметрической форме.
Постоянные интегрирования находятся по известным начальным условиям,
обозначаемым ![]() и
и 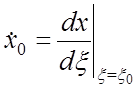 ;
;
![]() и
и 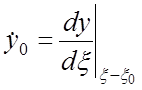 ,
и соответствующим моменту времени
,
и соответствующим моменту времени ![]() :
:
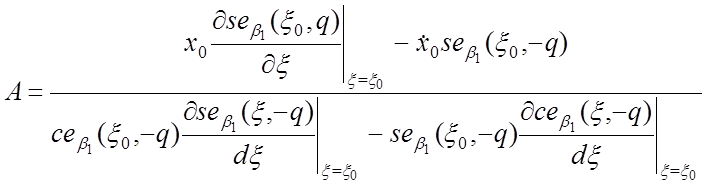 ;
(26)
;
(26)
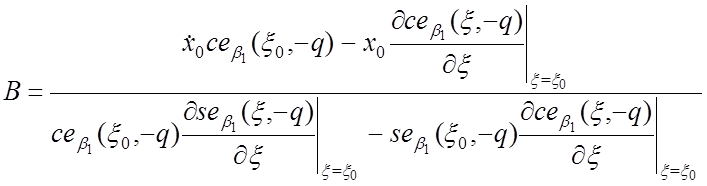 ;
(27)
;
(27)
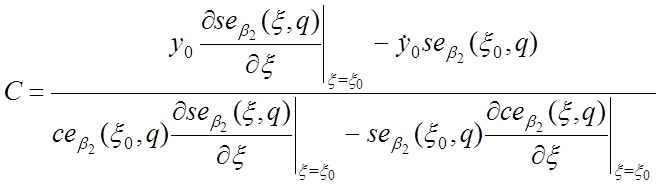 ;
(28)
;
(28)
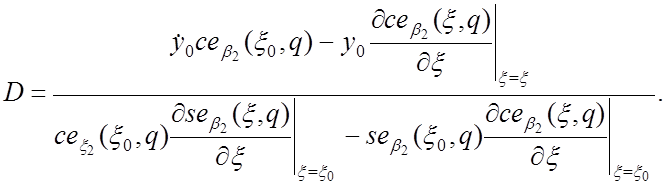 (29)
(29)
Соотношения (24)-(29) однозначно и точно определяют
траекторию стабильного иона в плоскости (x,y). Решение уравнения (14) идентично выражению (10),
которое при С5=![]() и С6=0
и для новой переменной
и С6=0
и для новой переменной ![]() имеет вид
имеет вид
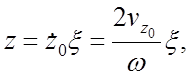 (30)
(30)
где 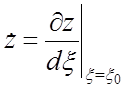 ;
; ![]() - составляющая начальной скорости
иона в направлении оси z при влете в анализатор.
- составляющая начальной скорости
иона в направлении оси z при влете в анализатор.
Для ионов с параметрами, соответствующими нестабильной
области диаграммы (a, q),
обозначенной двойной штриховкой (см. рис. 4), значение показателя ![]() в решении (17), зависящее от
значений a и q, действительно и в направлении x
равно
в решении (17), зависящее от
значений a и q, действительно и в направлении x
равно ![]() , а в направлении
, а в направлении ![]() равно
равно ![]() .
Аналитические выражения для параметров нестабильной траектории вытекают из выражения
(17) и имеют вид
.
Аналитические выражения для параметров нестабильной траектории вытекают из выражения
(17) и имеют вид
![]() (31)
(31)
![]() (32)
(32)
где функции ![]() и
и
![]() определяются, а
определяются, а ![]() и
и ![]() -
постоянные интегрирования. Составляющая нестабильной траектории вдоль оси
-
постоянные интегрирования. Составляющая нестабильной траектории вдоль оси ![]() по-прежнему определяется выражением
(30). Поскольку при нормальной работе анализатора область, обозначенная двойной
штриховкой, никогда не
по-прежнему определяется выражением
(30). Поскольку при нормальной работе анализатора область, обозначенная двойной
штриховкой, никогда не
пересекается прямой (18), а, напротив,
проходит ниже ее и пересекает область стабильных значений, или системой
выражений (25), (30) и (31), если параметры иона соответствуют точке (a, q), лежащей на прямой
(18) справа от области стабильных значений, или системой выражений (25), (30) и
(32), если точка (a, q)
лежит слева от области стабильных значений. В первом случае нестабильный ион
попадает на один из двух электродов анализатора, пересекающих ось х, во втором
– на один из двух электродов, пересекающих ось y
(см. рис. 1). Две группы постоянных интегрирования ![]() и
и
![]() , соответствующих первому и второму
случаям, рассчитывают с помощью соотношений, аналогичных выражениям (26)-(29).
, соответствующих первому и второму
случаям, рассчитывают с помощью соотношений, аналогичных выражениям (26)-(29).
Методику сколь угодно точного расчета значений ![]() и
и ![]() ,
а через них значений
,
а через них значений ![]() и
и ![]() входящих
в выражения для
входящих
в выражения для ![]() и
и ![]() ,
можно найти в [1].
,
можно найти в [1].
Качественно уже было показано, что разрешающая способность
квадрупольного масс-спектрометра тем выше, чем ближе к вершине диаграммы
стабильности (![]() ) (см. рис. 4) прямая (18),
пересекающая область стабильных значений (a,q). Из теории уравнения Матье [15] известно,
что чем ближе расположена точка (
) (см. рис. 4) прямая (18),
пересекающая область стабильных значений (a,q). Из теории уравнения Матье [15] известно,
что чем ближе расположена точка (![]() ). находящаяся в
области стабильности, к одной из границ этой области, тем меньше отличается
значение
). находящаяся в
области стабильности, к одной из границ этой области, тем меньше отличается
значение ![]() в выражениях (22) и (23) от 0 и 1.
Так, с приближением точки (
в выражениях (22) и (23) от 0 и 1.
Так, с приближением точки (![]() ) к правой границе
диаграммы стабильности значение
) к правой границе
диаграммы стабильности значение ![]() [см. уравнение (24)] увеличивается и стремится к 0. Из
сказанного следует, что должна существовать однозначная связь между разрешающей
способностью и значениями
[см. уравнение (24)] увеличивается и стремится к 0. Из
сказанного следует, что должна существовать однозначная связь между разрешающей
способностью и значениями ![]() и
и ![]() .
.
В [1]
получены зависимости ![]() - и
- и ![]() -параметров
траектории ионов от
-параметров
траектории ионов от ![]() в явном виде:
в явном виде:
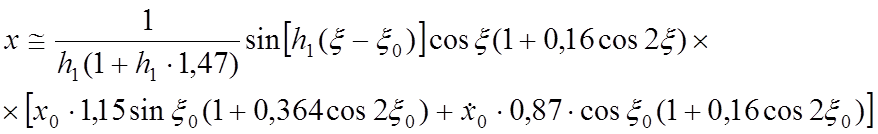
(33)
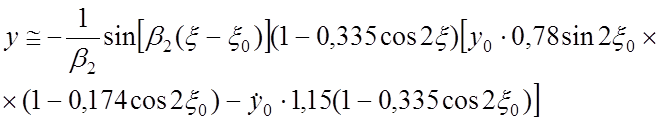 (34)
(34)
Характерное отличие между этими функциями заключается в
том, что х-параметр траектории иона меняет знак каждые ![]() , а y-параметр
через каждые
, а y-параметр
через каждые ![]() , что объясняется наличием
в выражении (33) сомножителя
, что объясняется наличием
в выражении (33) сомножителя ![]() перед квадратной
скобкой. Указанное отличие, практически никак не используемое в классическом
квадрупольном масс-спектрометре, делает возможным построение так называемого
однопольного масс-спектрометра, являющегося своеобразной модификацией
квадрупольного масс-спектрометра.
перед квадратной
скобкой. Указанное отличие, практически никак не используемое в классическом
квадрупольном масс-спектрометре, делает возможным построение так называемого
однопольного масс-спектрометра, являющегося своеобразной модификацией
квадрупольного масс-спектрометра.
Из анализа выражений (33) и (34) можно сделать следующие
выводы: отклонения стабильного иона от оси квадрупольного анализатора тем
больше, чем при прочих равных условиях больше угол влета иона относительно оси,
чем дальше от оси место влета и чем ближе точка, характеризующая ион на
диаграмме стабильности к одной из ее границ, т.е. чем меньше значения ![]() и
и ![]() .
.
Из перечисленных обстоятельств можно сделать вывод о необходимости ограничения определенными пределами начальных условий влета ионов, для того, чтобы обеспечить при анализе условия 100% прохождения стабильных ионов через анализатор. Это необходимо для облегчения количественной расшифровки полученного с помощью прибора спектра масс.
3. Условия фильтрации ионов
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.