Значение разрешающей способности КМ определяется
отрезком прямой ![]() , заключенным между двумя
границами стабильности (см. рис. 4). Из указанного рисунка ясно, что при
увеличении наклона этой прямой
, заключенным между двумя
границами стабильности (см. рис. 4). Из указанного рисунка ясно, что при
увеличении наклона этой прямой ![]() размеры данного
отрезка уменьшаются и, следовательно, уменьшается интервал масс ионов, летящих
при заданных напряжениях U, V по стабильным траекториям и
попадающих на вход приемника ионов, стоящего за квадрупольным анализатором. Для
расчета зависимости относительной разрешающей способности от величины
коэффициента
размеры данного
отрезка уменьшаются и, следовательно, уменьшается интервал масс ионов, летящих
при заданных напряжениях U, V по стабильным траекториям и
попадающих на вход приемника ионов, стоящего за квадрупольным анализатором. Для
расчета зависимости относительной разрешающей способности от величины
коэффициента ![]() необходимо воспользоваться
выражениями для собственных функций уравнений Матье (12) и (13) и
соответствующими уравнениями правой и левой границ стабильности на плоскости
значений (a, q) (см. рис. 4):
необходимо воспользоваться
выражениями для собственных функций уравнений Матье (12) и (13) и
соответствующими уравнениями правой и левой границ стабильности на плоскости
значений (a, q) (см. рис. 4):
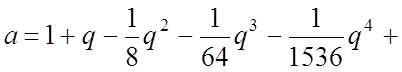 . . . (a>0, q<0); (47)
. . . (a>0, q<0); (47)
-a=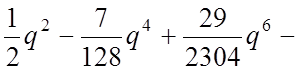 . . . (a<0, q>0). (48)
. . . (a<0, q>0). (48)
Совместным решением этих уравнений можно найти координаты точки пересечения двух границ стабильности, т.е. координаты вершины диаграммы стабильности на рис. 4.
a0=0,23699; q0=0,70600; ![]() (49)
(49)
При достаточно большой способности (![]() >100÷150) прямая
>100÷150) прямая ![]() отсекает от
диаграммы стабильности треугольник, размеры которого настолько малы, что
криволинейные стороны этого треугольника, описываемые выражениями (47) и (48),
вполне можно заменить отрезками прямых линий, исходящих из точки с координатами
(а0 и q0). Уравнения этих прямых, как известно, имеют
соответственно вид:
отсекает от
диаграммы стабильности треугольник, размеры которого настолько малы, что
криволинейные стороны этого треугольника, описываемые выражениями (47) и (48),
вполне можно заменить отрезками прямых линий, исходящих из точки с координатами
(а0 и q0). Уравнения этих прямых, как известно, имеют
соответственно вид:
a – a0 = Kx(q - q0) (50)
и
a – a0 = Ky(q - q0) (51)
где Kx и Ky – производные выражений (47) и (48) по qпри q=q0.
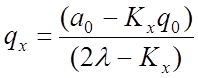 ;
;
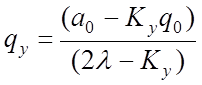 ,
(52)
,
(52)
можно найти величину относительной разрешающей способности:
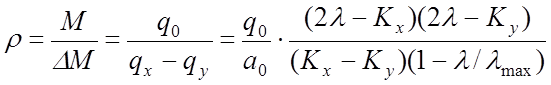 . (53)
. (53)
По расчету ![]()
![]() . Заменяя в числителе (53)
. Заменяя в числителе (53) ![]() на
на ![]() ,
что вполне соответствует точности проводимых вычислений, и, принимая во
внимание формулу (49), находится окончательно приближенное выражение для
относительной разрешающей способности КМ по уровню, близкому к основанию
соответствующего пика в спектре масс:
,
что вполне соответствует точности проводимых вычислений, и, принимая во
внимание формулу (49), находится окончательно приближенное выражение для
относительной разрешающей способности КМ по уровню, близкому к основанию
соответствующего пика в спектре масс:
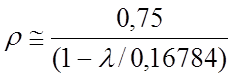 .
(54)
.
(54)
Из полученного выражения (54) можно сделать два важных
вывода: 1) при достаточно большой относительной разрешающей способности ![]() ее значение обратно пропорционально
степени близости отношения
ее значение обратно пропорционально
степени близости отношения ![]() к предельно
допустимой величине
к предельно
допустимой величине ![]() ; 2) абсолютная разрешающая
способность при заданном отношении
; 2) абсолютная разрешающая
способность при заданном отношении ![]() ухудшается (т.е.
ухудшается (т.е. ![]() увеличивается) пропорционально
номеру массы, поскольку из (54) следует:
увеличивается) пропорционально
номеру массы, поскольку из (54) следует:
![]() .
(55)
.
(55)
5. Зависимость абсолютной разрешающей способности КМ от энергии ионов и электрических параметров поля анализатора
Для достижения разрешающей способности ![]() на массе М ионы указанной
массы должны находиться в поле квадрупольного анализатора в течение некоторого
временного интервала tL, необходимого для того, чтобы ионы с массами
на массе М ионы указанной
массы должны находиться в поле квадрупольного анализатора в течение некоторого
временного интервала tL, необходимого для того, чтобы ионы с массами ![]() и
и ![]() ,
летящие по нестабильным траекториям, успели отклониться от оси анализатора на
расстояние большее, чем радиус поля, и, следовательно, осесть на стержни
анализатора. Отметим, что время tL, с,
пролета ионом с массой М, а.е.м., анализатора длиной L, см, при энергии поступательного движения иона
вдоль оси анализатора, определяемой разностью потенциалов пройденного ионом
ускоряющего электрического
,
летящие по нестабильным траекториям, успели отклониться от оси анализатора на
расстояние большее, чем радиус поля, и, следовательно, осесть на стержни
анализатора. Отметим, что время tL, с,
пролета ионом с массой М, а.е.м., анализатора длиной L, см, при энергии поступательного движения иона
вдоль оси анализатора, определяемой разностью потенциалов пройденного ионом
ускоряющего электрического
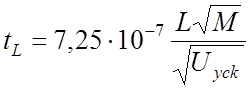 .
(56)
.
(56)
Это же время, выраженное в числе периодов (п) ВЧ электрического поля в квадрупольном анализаторе, изменяющегося с частотой f, Мгц, будет
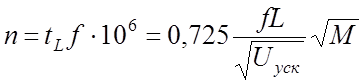 . (57)
. (57)
Величину разрешающей способности обычно оценивают
следующим образом. В теории масс-спектрометрии принято считать два соседних
пика с одинаковыми амплитудами разрешенными, если сигнал в провале между ними
не превышает определенного значения, составляющего некоторую долю ![]()
![]() 0,5
амплитуды пиков. При этом возможны два случая. Первый, когда ширина линии
спектра масс масс-спектрометра без учета хвостов, оцениваемая в данном случае
по формуле (55), больше разности между соседними разрешаемыми массами, и тогда
сигнал в провале между ними равен сумме потоков ионов двух соседних масс,
летящих по стабильным траекториям. Из этого следует, что в результате крутого
спада сигнала на границах импульсов даже незначительные взаимные перекрытия
соседних импульсов, составляющие 0,01 – 0,02 разности их масс, приводят к
резкому увеличению интегрального сигнала в провале между ними. Таким образом,
для качественного воспроизведения спектра ширина спектральной характеристики
без учета ее хвостов должна быть равна или меньше разности масс соседних
импульсов.
0,5
амплитуды пиков. При этом возможны два случая. Первый, когда ширина линии
спектра масс масс-спектрометра без учета хвостов, оцениваемая в данном случае
по формуле (55), больше разности между соседними разрешаемыми массами, и тогда
сигнал в провале между ними равен сумме потоков ионов двух соседних масс,
летящих по стабильным траекториям. Из этого следует, что в результате крутого
спада сигнала на границах импульсов даже незначительные взаимные перекрытия
соседних импульсов, составляющие 0,01 – 0,02 разности их масс, приводят к
резкому увеличению интегрального сигнала в провале между ними. Таким образом,
для качественного воспроизведения спектра ширина спектральной характеристики
без учета ее хвостов должна быть равна или меньше разности масс соседних
импульсов.
В случае, когда ширина спектральной характеристики, определяемой по формуле (55), равна разности масс, которые должны быть разрешены, величина сигнала в провале между соседними, одинаковыми по величине, импульсами, отнесенная к полному ионному току ионов данной массы, поступающему в анализатор, может быть рассчитана с помощью выражений (33) и (34).
С приближением к границам стабильности, как уже
упоминалось выше, значения h1 и ![]() стремятся к нулю, и в выражениях
(33) и (34) отношения
стремятся к нулю, и в выражениях
(33) и (34) отношения ![]() и
и ![]() окажутся
равными в пределе следующей величины:
окажутся
равными в пределе следующей величины:
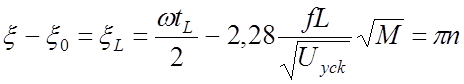 , (58)
, (58)
где tL и nопределяются соответственно выражениями (56) и (57).
Отношение амплитуды импульса спектра масс к сигналу в
провале между импульсами, определяющее качество разрешения масс-спектрометра, в
диапазоне масс М<Мгр (когда
трансмиссия ![]() ) равно
) равно
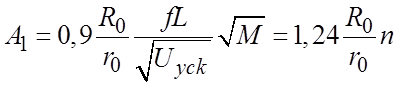 , (59)
, (59)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.