Элементы расчета и конструирования гиперболоидного масс-спектрометра типа «Фильтр масс»: Учебное пособие к курсовому проектированию, страница 3

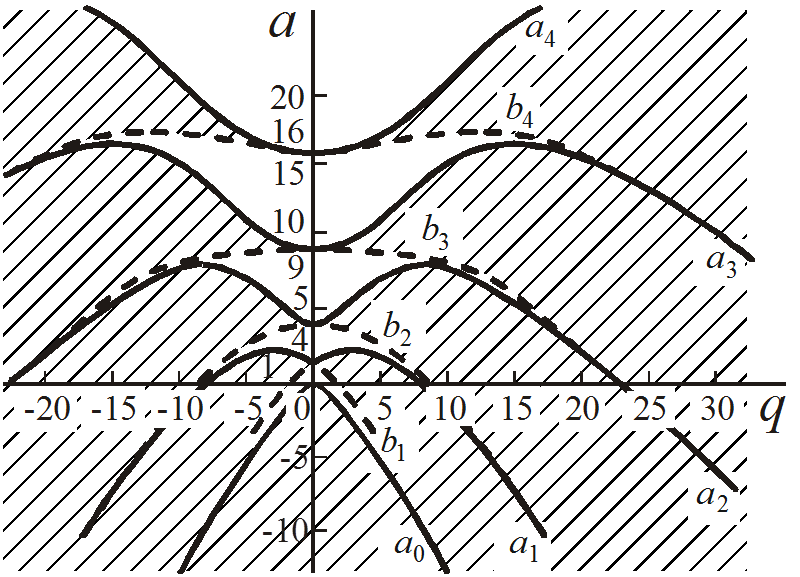
Если затем наложить друг на друга зеркальные отображения относительно осей а и q (см. рис. 2), то получим диаграмму стабильности одновременно

Рис. 2. Диаграмма стабильности уравнения Матье в

канонической форме

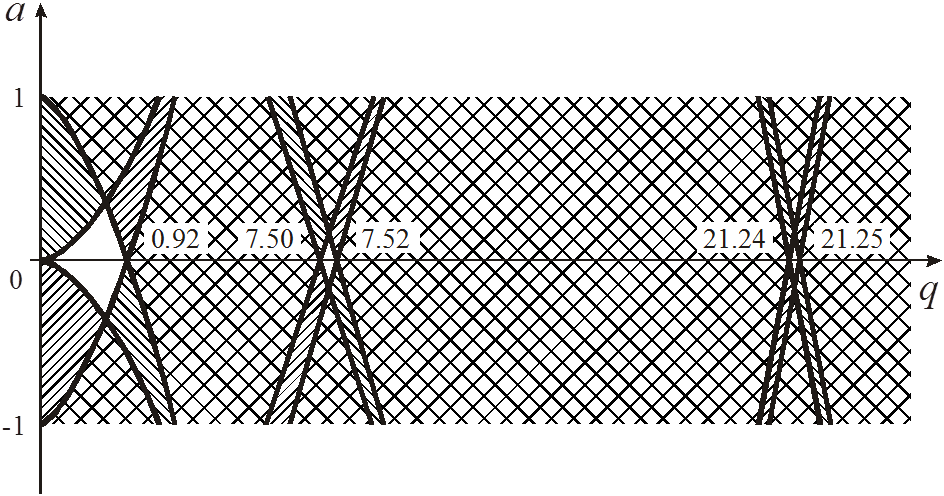Рис. 3. Совмещённая диаграмма стабильности

уравнений Матье (12) и (13)

двух уравнений Матье (12) и (13) (рис. 3). Незаштрихованные участки на данном рисунке соответствуют устойчивым решениям этих уравнений. Наличие на диаграмме области стабильных решений физически означает возможность для иона со «стабильной» траекторией, отклонения которой от оси конденсатора ограничены, пройти этот конденсатор из конца в конец. Траектории всех остальных ионов, попавших в области, обозначенные на рис. 3 одинарной или двойной штриховкой, «нестабильны», т.е. отклонения их от оси конденсатора со временем неограниченно возрастают вдоль оси xили y, одинарная штриховка, или в обоих направлениях одновременно, двойная штриховка. Другими словами, квадрупольный конденсатор с напряжением вида (11) на его электродах может обладать избирательностью по массам и, следовательно, его можно использовать в качестве анализатора в аналитической части масс-спектрометра.

Из бесконечного числа областей со стабильными решениями (см. рис. 3), в каждой из которых в принципе возможна нормальная работа квадрупольного масс-спектрометра, удобнее всего работать в области, расположенной вблизи начала координат диаграммы (a, q). Ведь чем меньше значения коэффициентов a и q, тем меньше в соответствии с выражениями (15) требующиеся для анализа ионов с массой m постоянное (U) и переменное (V) напряжения, подводимые к электродам анализатора. Вместе с тем вблизи начала координат можно работать в широком диапазоне масс, практически без паразитных сигналов, создаваемых ионами других масс, попавшими в удаленные от начала координат (a, q) стабильные области, расположенные в основном вдоль оси q. Если же работать в одной из этих удаленных областей, то в спектре масс постоянно будут присутствовать паразитные сигналы за счет стабильной области около начала координат. Есть и другие преимущества работы в указанной области стабильности, которые будут рассмотрены далее. 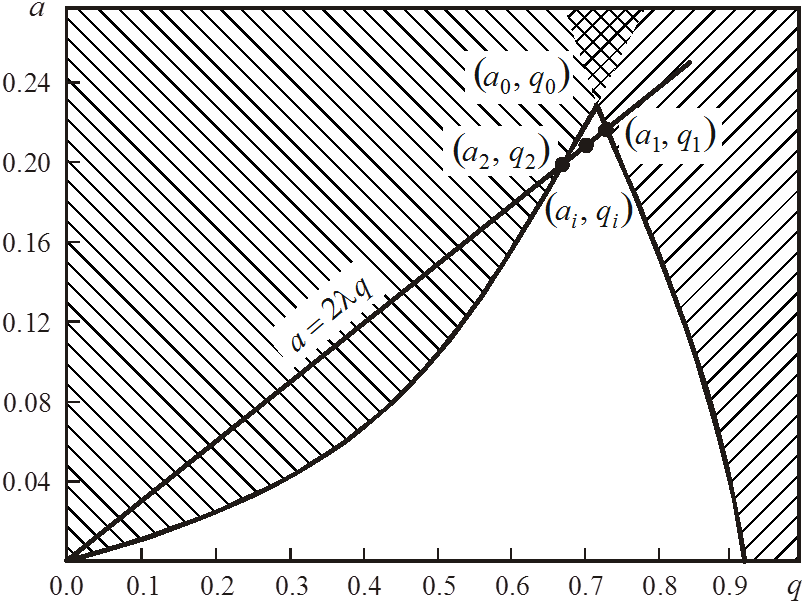На рис. 4 в укрупненном масштабе изображена выбранная на диаграмме (a, q) область стабильности, расположенная вблизи начала координат. Легко убедиться в наличии избирательности по массам у квадрупольного анализатора, а также понять принцип его работы в режиме сканирования по спектру масс. Выберем внутри области стабильности произвольную точку с координатами (a_i, q_i). Этой точке при заданных значениях радиуса поля анализатора r₀ , частоты ВЧ колебаний и напряжений U и V соответствует такая величина массы m_i, при которой однозарядный положительный ион, выпущенный из ионного источника в анализатор параллельно оси z, полетит по стабильной траектории, пройдет весь анализатор и достигнет приемника ионов, стоящего за анализатором. Если со временем ни один из параметров анализатора не изменится (т.е. останутся постоянными значения U V r₀), то в приемник ионов попадут и просуммируются в общем токе все ионы с массами в диапазоне m₁<m<m₂. Значения m₁ и m₂ соответствуют точкам пересечения прямой, проходящей через начало координат и точку (a_i, q_i), с границами области стабильности. Уравнение этой прямой можно записать в виде

 

 

Рис. 4. Первая область диаграммы стабильности

уравнений Матье (12) и (13)

                                              a = 2q,                                                             (18)

где = a_i/2q_i=U_i/V_i. Точки пересечения прямой и границ области стабильности (см. рис. 4) имеют координаты (a₁, q₁) и (a₂, q₂). Пользуясь соотношениями (15), можно рассчитать границы интервала масс ионов, пропускаемых квадрупольным анализатором, m₁ и m₂:

 

                                  m₁=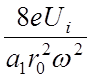       или         =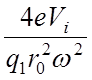

                                                                                                 .                                (19)

                                  m₂=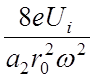    или           =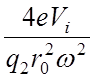 

Увеличивая угол наклона прямой  a = 2q с помощью соответствующего выбора значений U и V, можно сократить интервал прозрачности анализатора (m₁ , m₂) теоретически до такой сколь угодно малой величины, чтобы через анализатор проходили ионы лишь строго определенной массы, а все остальные оседали на его электродах. Из приведенных рассуждений следует, что разрешающая способность квадрупольного масс-спектрометра по массам зависит от наклона прямой a=2q, т.е. от значения . Выше была рассмотрена работа анализатора в режиме слежения за ионами определенной массы. Если изменять во времени один из параметров анализатора, например частоту  или напряжения U  и V , то регистрирующее устройство зафиксирует спектр масс, представляющий собой последовательность импульсов. Каждый импульс будет соответствовать определенному номеру массы, а его амплитуда – парциальному содержанию данного компонента в анализируемой смеси веществ. Развертку спектра масс в большинстве случаев осуществляют пропорциональным изменением  значений U  и V при сохранении неизменным отношения между ними (=const). При этом технически проще обеспечить линейную шкалу по массам, а также добиться максимально широкого диапазона анализа по массам за один цикл развертки.

Отметим в заключение, что точкам прямой (18) на диаграмме (a, q) (см. рис. 4) при заданных параметрах анализатора соответствуют ионы разных масс, причем, чем больше масса иона, тем ближе к началу координат плоскости (a, q) располагается на этой прямой соответствующая данному иону точка.

2.  Аналитические выражения для стабильных ионов в поле квадрупольного анализатора

Для определения основных параметров масс-спектрометра необходимо знать вид стабильных и нестабильных траекторий ионов в квадрупольном анализаторе, а также факторы, влияющие на их форму.