Элементы расчета и конструирования гиперболоидного масс-спектрометра типа «Фильтр масс»: Учебное пособие к курсовому проектированию, страница 14

1. Взаимно независимые нестабильности величин ,  и  влияют на возможность реализации заданной разрешающей способности в КМ. В режиме непрерывного слежения эти нестабильности способствуют неконтролируемой перестройке КМ с выбранной для слежения массы на соседние массы или блуждания в пределах выбранного пика спектра масс, что приводит к возникновению паразитных изменений выходного сигнала, создающих дополнительные помехи. Из выражения в примечании к формуле (114) при  находим соотношение:

                                                                             (123)

и аналогичное ему (после нахождения полного дифференциала величины )

                                    .                                        (124)

Из формул (123) и (124) следует, что для реализации заданной разрешающей способности  при  необходимо, чтобы, по крайней мере,

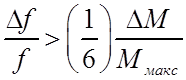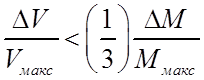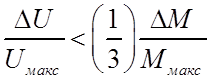         ;  ;  ,                 (125)

где ,  и  – максимальные изменения ,  и  соответственно. Однако для того чтобы в режиме непрерывного слежения за парциальным содержанием какой-либо компоненты в анализируемой смеси веществ паразитные изменения сигнала составляли не более -й доли сигнала в максимуме соответствующего пика, необходимо, полагая для простоты, что импульс спектра масс имеет форму, близкую к равностороннему треугольнику, чтобы

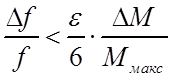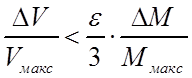            ;  ; и 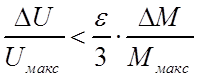.        (126)

2. От стабильности поддержания выбранного отношения  зависит разрешающая способность КМ. Так, согласно (54),

                                  ,                                           (127)

откуда при

                                        .                                              (128)

Из формулы (128) следует, что при  и  . Учитывая, что , должно быть

                                       .                                       (129)

Из сопоставления (128) и (129) найдём

                           ,                              (130)

что при  соответствует на порядок более жёстким требованиям к стабильности  и , чем по (125), и примерно совпадает с требованиями по (126).

Из этого вытекает, что при конструировании ГВЧ нужно прибегать к таким техническим решениям, которые бы определялись необходимостью создания однозначной линейной функциональной связи между величинами  и , с тем, чтобы случайные изменения одной из них вели к немедленным пропорциональным изменениям другой.

3. Пульсации напряжений  и  можно отнести к разряду нестабильностей, имеющих регулярный характер и вызванных, например, пульсациями на выходах выпрямителей, питающих ГВЧ, сетевыми или какими-либо другими наводками на цепи ГВЧ. Зависимость значения  от времени  при линейном законе развёртки спектра масс и наличии упомянутых пульсаций можно выразить таким образом:

                                при .                                       (131)

Здесь  и  – постоянные, имеющие следующие значения:

                                              

и                                                                                                                              (132)

                             ;

 – достаточно гладкая периодическая функция времени, характеризующая пульсации. Ясно, что если длительность отдельных пульсаций меньше длительности импульса спектра масс и

                                            ,                                                      (133)

то будут наблюдаться расчленение импульса спектра масс и уменьшение его амплитуды, то есть потеря чувствительности из-за недопустимого увеличения ширины частотного спектра сигнала. При

                                                                                                       (134)

также наблюдается потеря чувствительности в результате уменьшения длительности импульса спектра масс. На вершине импульса при этом могут образоваться выбросы и провалы. В промежуточном случае, когда

                                         ,                                          (135)

должны наблюдаться некоторое увеличение длительности импульсов спектра масс и искажение их формы. Из выражения (135) ясно, что для того чтобы изменения длительности импульса спектра масс, вызванные пульсациями выходного напряжения ГВЧ, были меньше -й доли от номинальной величины, равной , необходимо соблюдение неравенства

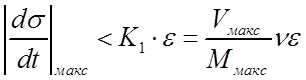                                       .                                     (136)

Полагая для примера, что пульсации имеют вид синусоиды , из (136) находим выражение для максимально допустимого значения амплитуды пульсаций напряжения :

                                  ,                                       (137)

где  – круговая частота пульсаций, гц. Если положить  Гц;  а.е.м./с и , то при известных  В и  а.е.м. получим  меньше 0,21 В, что при  В даёт величину относительной пульсации вблизи верхней границы диапазона анализируемых масс 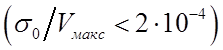. Условия (136) и (137) имеют смысл при . Если , то они могут быть ослаблены и примут вид

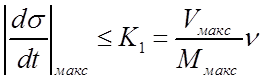                                                                                   (138)

и при

                                       .                                        (139)

Соблюдение условий (138) и (139) гарантирует КМ от ухудшения разрешающей способности на тяжёлых массах. Физически условия (138) и (139) означают, что пульсации не способны вызвать такие изменения в законе нарастания напряжения  [см. выражение (131)], при которых бы крутизна нарастания во времени становилась отрицательной. В случае если это всё же имеет место, то есть требование (138) нарушено, то абсолютная разрешающая способность при наличии пульсаций

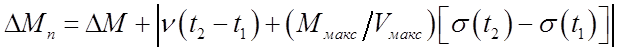              .                   (140)

Здесь  определено формулой (55), а  и  – корни уравнения

                                    ,                                          (141)

такие, что в интервале  левая часть уравнения (141) отрицательна.

При  выражение (140) преобразуется к виду