В основу разработки данного учебного пособия положены результаты, приведенные в работе [1].
1. Принцип действия квадрупольного фильтра масс (КМ)
Общие принципы
построения масс-спектрометров широко известны из литературы [1, 2, 11-13]. КМ относится к группе так называемых динамических
приборов с последовательным во времени анализом спектра масс. Как и в любом
другом масс-спектрометре, аналитическая часть его, ответственная за выработку
сигналов спектра масс, содержит ионный источник, анализатор и приемник ионов.
Названием своим этот прибор обязан электростатическому квадрупольному
конденсатору [14], который используется в нем в качестве
анализатора («фильтра масс») его аналитической части. Квадрупольный конденсатор
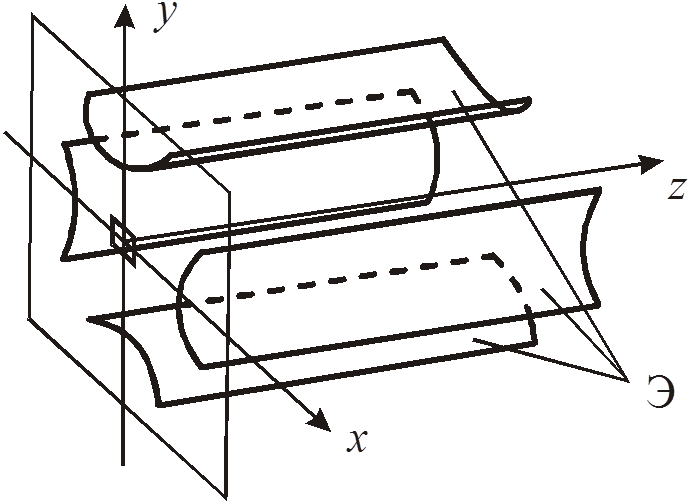
(рис. 1) состоит из четырех, расположенных параллельно друг другу, проводящих
поверхностей (в поперечном сечении они имеют форму гипербол), к которым попарно
приложено электрическое напряжение и. Квадрупольный конденсатор способен
выполнять функции анализатора ионов по их массам лишь при строго определенном
виде создаваемого внутри него электрического поля. Выясним, каким должно быть
напряжение и, для того чтобы из всех ионов, впущенных узким пучком в
конденсатор вдоль его оси (см. рис. 1, ось z),
до выхода конденсатора долетели лишь ионы с массой m.
Потенциал ![]() в поле квадрупольного конденсатора
без учета краевых эффектов [14] имеет вид
в поле квадрупольного конденсатора
без учета краевых эффектов [14] имеет вид
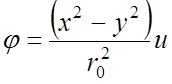 , (1)
, (1)
где x и y – координаты плоскости, перпендикулярной к оси конденсатора (совпадает с осью z), причем начало координат расположено на входе анализатора; r0 – кратчайшее расстояние от оси анализатора до любого из электродов. Две асимптотические по отношению к электродам конденсатора плоскости, пересекающиеся по оси z, имеют нулевой или некоторый постоянный относительно корпуса прибора потенциал.
Составляющие напряженности электрического поля Ex, Ey, и Ez по осям x, y, z определяются следующими соотношениями:
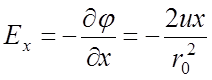 ;
(2)
;
(2)
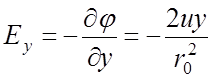 ;
(3)
;
(3)
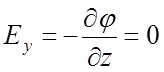 . (4)
. (4)
 |
а
 |
б
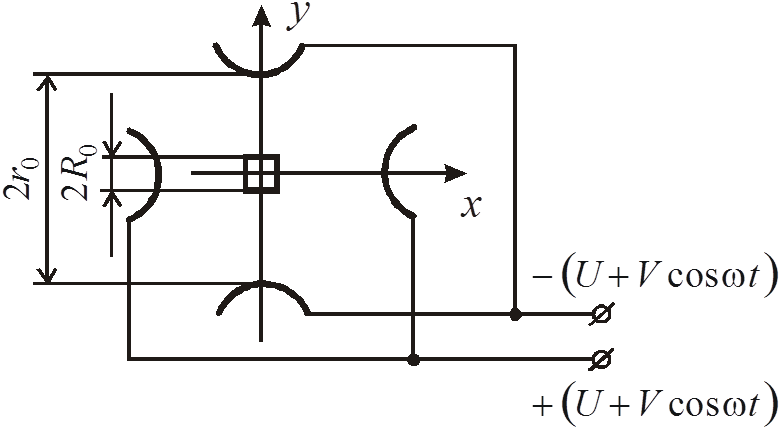
Рис.1. Квадрупольный конденсатор (xy – плоскость входной апертуры анализатора; Э – полеобразующие электроды):
а – внешний вид; б – схема подачи напряжения на полеобразующие электроды.
Если ионы анализируемого вещества с массой mi направить в квадрупольный конденсатор вдоль оси z с некоторой начальной скоростью, vi, то их движение будет описываться системой уравнений Ньютона:
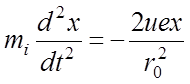 ; (5)
; (5)
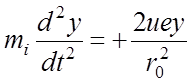 ; (6)
; (6)
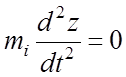 , (7)
, (7)
где t – время, а е –
заряд иона. Решения уравнений (5) – (7) являются аналитическим выражением
траектории иона в конденсаторе, заданной в параметрической форме. При u=const![]() 0
они имеют следующий вид:
0
они имеют следующий вид:
![]() ;
(8)
;
(8)
![]() ;
(9)
;
(9)
![]() (10)
(10)
где С1 – С6 – постоянные интегрирования,
определяемые из начальных условий, а 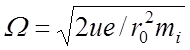 . В данном случае
решение уравнения (9) оказывается неограниченно возрастающим, т.е. все ионы
независимо от их массы через некоторый промежуток времени попадут на электроды,
пересекающие ось y. Это означает, что
квадрупольный конденсатор с постоянным напряжением на его электродах не
обладает свойствами избирательности по отношению к ионам какой-то определенной
массы m и потому не может служить анализатором
масс-спектрометра.
. В данном случае
решение уравнения (9) оказывается неограниченно возрастающим, т.е. все ионы
независимо от их массы через некоторый промежуток времени попадут на электроды,
пересекающие ось y. Это означает, что
квадрупольный конденсатор с постоянным напряжением на его электродах не
обладает свойствами избирательности по отношению к ионам какой-то определенной
массы m и потому не может служить анализатором
масс-спектрометра.
Допустим теперь, что на электроды конденсатора подано напряжение вида
![]() ,
(11)
,
(11)
где ![]() - угловая частота. В этом случае
уравнения (5) – (7) можно привести к виду:
- угловая частота. В этом случае
уравнения (5) – (7) можно привести к виду:
![]() ;
(12)
;
(12)
![]() ;
(13)
;
(13)
![]() ;
(14)
;
(14)
где
![]()
![]() ;
; ![]() (15)
(15)
![]() и
и ![]() -
вторые производные координат x, y, z по новой независимой
безразмерной переменной
-
вторые производные координат x, y, z по новой независимой
безразмерной переменной ![]() .
.
Уравнения (12) и (13) относятся к так называемым уравнениям Матье, теория которых достаточно полно изложена в работе [15]. Уравнение Матье в канонической форме имеет вид
![]() .
(16)
.
(16)
Общее решение его, согласно работе [20], представляется в виде суммы двух рядов:
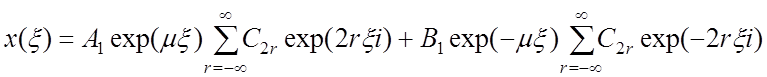 , (17)
, (17)
где A1 и B1 – произвольные постоянные; i = ![]() ;
; ![]() - в общем случае комплексно; C2r – постоянный коэффициент ряда (17), напоминающего ряд
Фурье.
- в общем случае комплексно; C2r – постоянный коэффициент ряда (17), напоминающего ряд
Фурье.
Решение
(17) имеет следующие свойства: а) оно неустойчиво (т.е. x![]() при
при ![]() ),
если в общем случае
),
если в общем случае ![]() при
при ![]() >0
и любом действительном
>0
и любом действительном ![]() ; б) решение устойчиво
(т.е. x ограничено или
; б) решение устойчиво
(т.е. x ограничено или ![]() 0
при
0
при ![]() ), если
), если ![]() ,
где
,
где ![]() - произвольное целое число; 0<
- произвольное целое число; 0<![]() <1, причем решение периодично, если
<1, причем решение периодично, если ![]() - рациональная дробь, и непериодично,
если
- рациональная дробь, и непериодично,
если ![]() иррационально.
иррационально.
На плоскости значений a и q можно построить диаграмму стабильности (рис. 2), разбивающую эту плоскость на несколько частей, одни из которых заштрихованные, соответствуют нестабильным решениям уравнения (16), а другие, незаштрихованные, - стабильным. Характеристические кривые am, bm+1 (m=0, 1, 2, …), разделяющие диаграмму (a, q) на стабильные и нестабильные участки, представляют собой зависимости собственных значений функций Матье целого порядка от q [15].
Зная диаграмму стабильности канонического уравнения (16), нетрудно представить себе начертание аналогичных диаграмм для уравнений (12) и (13). Для выражения (12) эту диаграмму можно получить из рис. 2, зеркально отобразив его относительно оси а, поскольку перед вторым слагаемым в скобках в уравнении (12) в отличие от уравнения (16) стоит знак «+». Диаграмма стабильности уравнения (13) по аналогичным причинам получится зеркальным отображением рис. 2 относительно оси q.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.