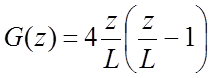Элементы расчета и конструирования гиперболоидного масс-спектрометра типа «Фильтр масс»: Учебное пособие к курсовому проектированию, страница 12

                              .                                              (95)

Отметим, кстати, что замена гиперболических электродов круглыми цилиндрическими, если она выполнена оптимальным образом [8, 14][т.е. радиус стержней лежит в пределах (1,11-1,16) r₀], приводит к искажениям поля второго и более высоких порядков малости, которыми можно пренебречь.

9.2. Максимально допустимая непараллельность электродов анализатора

Имея в виду, что  - величина малая по сравнению с 1, найдем выражения для уравнений движения поля, опуская в них величины второго и более высоких порядков малости с величиной :

                                               (96)

                                                 (97)

               .                                       (98)

Из полученного результата можно сделать следующие выводы: 1) по виду уравнения (98) можно предположить кардинальные различия в характере движения ионов вдоль оси z, влетающих в анализатор в разных квадрантах, для которых будет выполняться условие

                                                     x² >y²                                                           (99) или

                                                    x² <y²                                                        (100) 2) приближенное решение уравнения (98) можно найти, подставляя в его правую часть решения однородных уравнений Матье (12) и (13), поскольку добавочные члены, создаваемые в решениях уравнений (96) и (97) малой правой частью всегда тоже малы. Обозначим через x²_пост и у²_пост постоянные слагаемые в круглых скобках правой части выражения (96). Указанные составляющие создают в решении уравнения (96) секулярные члены, доминирующие над прочими слагаемыми, которые в дальнейшем можно будет опустить из-за их малости по сравнению с секулярными членами.

Перейдем к рассмотрению двух упомянутых выше случаев типичных искажений поля в анализаторе. После подстановки (94) в (96) – (98) находим:

                                            (101)

                                              (102)

                                               (103) Решение уравнения (103) при фиксированных x²_пост и у²_пост имеет вид:

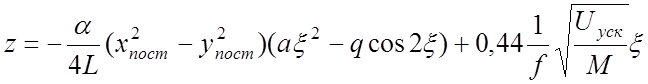                 .                  (104) Очевидно, что

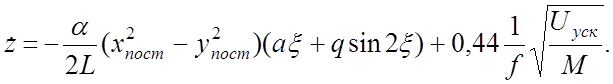                                         (105)

Заметим, что при самых неблагоприятных условиях, когда (x²_пост - у²_пост)= и   если

                               <                                          (106) z – составляющая вектора скорости иона во время пролета им анализатора t_L не изменяет своего направления, т.е. движение вдоль оси z осуществляется с переменной по величине скоростью без изменения ее знака. Если же

                                0,1>>1.64U_уск/,                                        (107) то может наступить момент, когда ион прекратит движение в анализаторе в направлении оси z и полетит обратно от приемника ионов в сторону ионного источника.

Оценим реальность описанной ситуации. При U_уск 10в; f=3 МГц; М=10³ а.е.м.;  получим . Из определения , данного в (93), при G(z)=G_макс=1

                                              ,                                                  (108)  где - максимальное отклонение радиуса поля от номинала.

Реальные возможности производства достаточно просто позволяют обеспечивать (при отношении длины анализатора к диаметру стержня не более 30-40) величину «(4÷5)·10^-3 и меньше, т.е. (4÷5)·10^-3, что обусловливает заведомое выполнение условия (106). Нарушение (96) и, следовательно, удовлетворение условию (107) возможны лишь в приборах, в которых реализуются режимы, близкие к предельным, т.е. при весьма высоких разрешающих способностях или больших массовых числах анализируемых ионов. Нарушение (106) приводит к резкому ухудшению основных характеристик КМ: его чувствительности и разрешающей способности из-за возникновения ситуации, способствующей образованию значительного объемного заряда внутри анализатора из накапливающихся положительно заряженных ионов. Это касается лишь тех ионов, для которых x²_пост - у²_пост>0. Для всех прочих ионов (x²_пост - у²_пост<0) наблюдается ускорение их в направлении оси z по мере приближения к концу анализатора.

Имея в виду, что для КМ с обычными характеристиками условие (106) выполняется с запасом, по крайней мере, на порядок, можно считать, что

                                                                     (109) где ^<_>0 – малая величина, которой в дальнейшем пренебрежем. Тогда

                              .                                  (110) Подставляя (110) в (101) и (102), получаем параметрические выражения движения иона в плоскостях xz и yz. Решениями уравнений (101) и (102) будут выражения, которые после преобразований и упрощений для случая можно привести к виду:

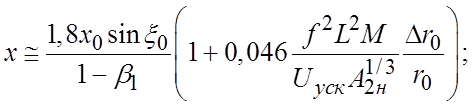                                                     (111)

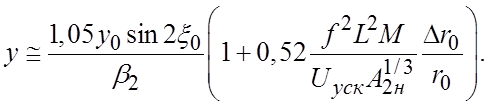                                                   (112)

Можно получить условие, определяющее величину максимально допустимого симметричного относительно оси анализатора расхождения (или схождения) внутренних поверхностей полеобразующих электродов:

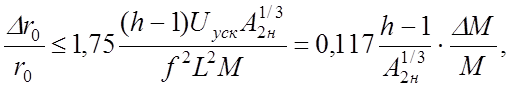                                           (113) где  - величина допустимого относительного уменьшения ионного тока на выходе анализатора, вызванного указанным искажением поля.

Сравнивая формулу (113) со следующим соотношением [6-8]

                                                                              (114) можно заключить, что выражение (114) справедливо для частного случая, соответствующего значению отношения , что при А_2н=20 дает .

Из выражения (113) видно, что предельно допустимое линейное отклонение радиуса поля от номинального значения обратно пропорционально относительной разрешающей способности КМ, реализуемой на уровне (1/А_2н)·100 % от амплитуды импульса спектра масс рассматриваемой массы.