Элементы расчета и конструирования гиперболоидного масс-спектрометра типа «Фильтр масс»: Учебное пособие к курсовому проектированию, страница 5

Как уже отмечалось, функция квадрупольного конденсатора как анализатора масс-спектрометра состоит в том, чтобы пропускать на коллектор приемника ионов (отфильтровывать) по возможности все ионы со стабильными траекториями и улавливать все прочие ионы, у которых хотя бы один из параметров траектории (вдоль оси х и у) нестабилен. Первое требование может быть удовлетворено лишь в том случае, если максимальное отклонение стабильной траектории от оси анализатора меньше радиуса поля r₀. Иначе ион со стабильной траекторией попадает на один из электродов анализатора и не достигнет приемника ионов. Второе требование будет удовлетворено, если отклонение нестабильной траектории от оси анализатора во время пролета иона через анализатор превзойдет величину радиуса поля r₀.

Максимальные отклонения стабильных х- и у-параметров траектории иона от оси анализатора можно рассчитать, пользуясь решениями (24) и (25):

                                    х_макс=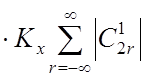;                                      (35)

                                   у_макс=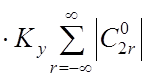;                                      (36)

где коэффициенты A, B, C, D определяются выражениями (26) – (29);  и  - рассчитываются по известной методике, изложенной в [9].

Вводя обозначения

                                                                                                                                   

                                                                                          (37)

и выполняя указанные в (35) и (36) алгебраические действия, определяем

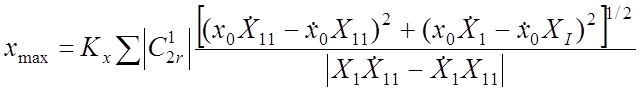                  ,                    (38)    

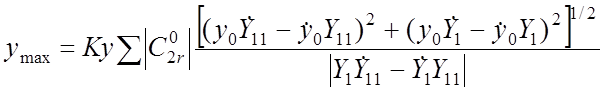                    .                       (39)

Значения  при заданном  строго определены коэффициентами а и q.

Если положить в выражениях (38)  (39)  и  (r₀ – радиус поля квадрупольного конденсатора), то можно найти два определенных соотношения, связывающие между собой начальные условия влета иона в анализатор по оси и  и  и . При этом стабильный ион еще способен пройти анализатор и попасть в приемник ионов. Уравнения (38) и (39) с учетом сделанных замечаний можно преобразовать к виду:

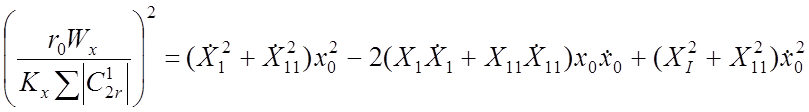        ;      (40)

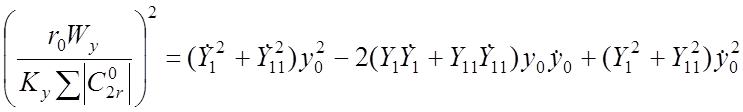       ;                (41)

Выражения, стоящие в круглых скобках в правых и левых частях равенств (40) и (41), не зависят от начальных координат (x₀,y₀) и от углов влета иона в анализатор . Нетрудно убедиться, что кривые второго порядка, описываемые выражениями (40) и (41), являются эллипсами относительно  и . На рис. 5 изображено три семейства эллипсов для разных  в координатах  [8]. Параметром в каждом семействе служит начальная фаза влета иона в анализатор , равная  3/4, 0, . Если начальные условия  соответствуют точкам, расположенным внутри эллипса, то максимальное отклонение стабильной траектории от оси квадрупольного анализатора будет меньше . Из рис. 5 видно, что максимальное отклонение для всех начальных фаз превосходит начальную координату и только при  () равно ей. Это означает, что для входа ионов в анализатор можно использовать лишь некоторую небольшую область поперечного сечения поля анализатора, расположенную вблизи начала координат (см. рис. 1) и имеющую размеры, много меньшие величины 2r₀(2x_max и 2y_max), причем углы влета ионов в анализатор не должны превышать некоторого максимально возможного значения и .

Рис. 5. Допустимые начальные условия влёта ионов в анализатор для различных рабочих точек  и фаз влёта :

а – ;  б – ;  в – ;  г – .

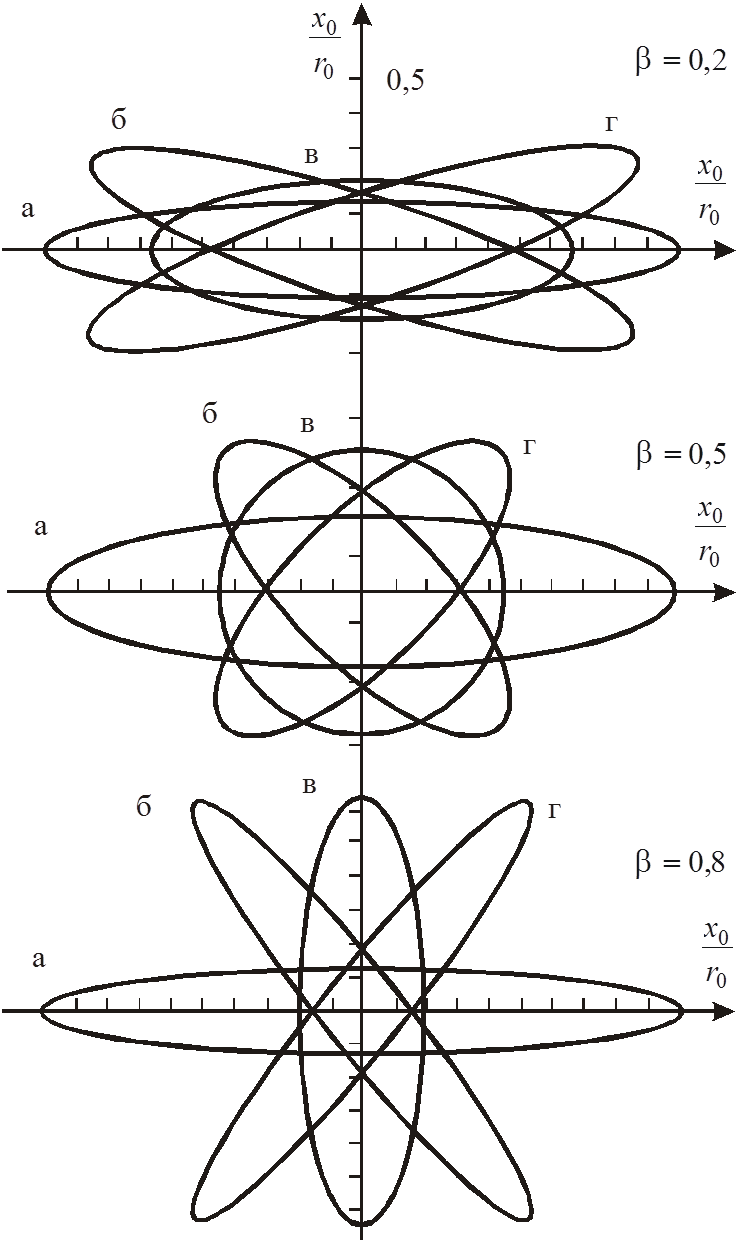Пользоваться выражениями (38) и (39) для определения максимального отклонения траектории стабильного иона от оси анализатора в плоскостях xz и yz неудобно. Однако при <<1 и <<1 (наблюдается при среднем и тем более высоком разрешении) ряды, входящие в выражения , быстро сходятся и могут быть с достаточной степенью точности определены несколькими первыми членами, что значительно упрощает выполнение различных оценочных расчетов. Учитывая сделанные замечания, выражения (38) и (39) можно упростить следующим образом:

         

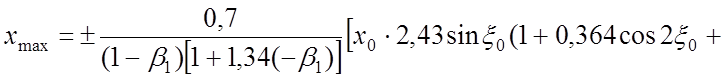
                                                                               (42)

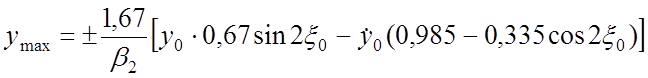              ;                       (43)

Из анализа выражений (42) и (43) видно, что экстремальные параметры траектории существенно зависят не только от параметров  и , но и от фазы влета иона в анализатор по осям х и у.

Из сопоставления условий  прохождения стабильными ионами квадрупольного анализатора

                                                 и                                                 (44)

и выражений (42) и (43) можно найти соотношения, которым должны удовлетворять начальные координаты стабильных ионов, соответствующие моменту влета их в анализатор:

                                     < ;

                                     < ;

                                     < ;

                                     < .

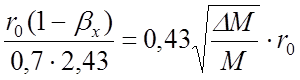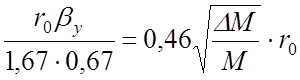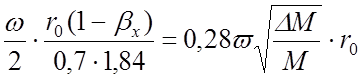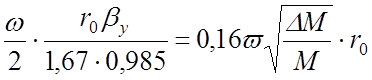Поскольку ионно-оптическая система источника осесимметрична, требования к начальным условиям влета ионов в анализатор будут следующие:

                                       < 0,43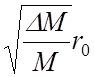

или, что то же самое:

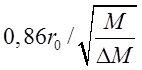                                            <                                                  (45)    

(D и R₀ – соответственно диаметр и радиус входной апертуры анализатора) и

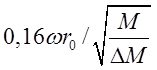                                      и < .                                         (46)

4. Зависимость относительной разрешающей

способности КМ от отношения  l=U/V

Для определения разрешающей способности любого масс-спектрометра необходимо точно знать форму его спектральной характеристики или (что то же самое) форму отдельного импульса (линии) спектра масс с учетом обоих его хвостов.

Мерой абсолютной разрешающей способности является ширина линии спектра масс , а е.м., измеренная на определенном уровне от основания соответствующего пика относительно его амплитуды. Относительная разрешающая способность масс-спектрометра  равна отношению массы измеряемого пика М к ширине линии данной массы , т.е. к величине абсолютной разрешающей способности ().