Замедляющие системы (основные свойства, характеристики, теоретические и экспериментальные методы исследования замедляющих систем): Учебное пособие

Федеральное агентство по образованию

Рязанский государственный радиотехнический университет

А.А. ШИШКОВ

ЗАМЕДЛЯЮЩИЕ СИСТЕМЫ

Учебное пособие

Рязань 2006

УДК 621. 385.6: 621. 372. 81

          Замедляющие системы: Учеб. пособие/ А.А. Шишков; Рязан. гос. радиотехн. ун-т. Рязань, 2006. 52 с.     

          Приведены конструкции, изложены основные свойства, характеристики, теоретические и экспериментальные методы исследования замедляющих систем.

         Предназначено для студентов специальностей 200300, 071400 направления  654100 и направления 550700.

         Компьютерная верстка выполнена Н.О. Давыденковой.

         Ил. 28. Библиогр.: 11 назв.

             Электромагнитные волны , замедляющие системы, дисперсионные характеристики, сопротивление связи, измерения

           Печатается по решению редакционно–издательского совета Рязанского государственного радиотехнического университета.

           Рецензент: кафедра ЭП Рязанского государственного радиотехнического университета. (зав. кафедрой д-р техн. наук, проф. В.К. Федяев)

Ш и ш к о в Александр Александрович

Замедляющие системы

 Редактор М.Е. Цветкова 

    Корректор С.В. Макушина

Подписано в печать 05.06.06. Формат бумаги 60 х 84 1/16.

Бумага газетная. Печать трафаретная. Усл. печ. л. 3,25

Уч.-изд. л. 3,25. Тираж 60 экз. Заказ

Рязанский государственный радиотехнический университет.

390005, Рязань, ул. Гагарина, 59/1.

Редакционно-издательский центр РГРТУ.

     © Рязанский государственный

 радиотехнический университет, 2006

Введение

В микроволновой технике находит широкое применение класс электронных приборов, принцип действия которых основан на длительном взаимодействии электромагнитной волны с электронным потоком. Для эффективного взаимодействия и обмена энергией между электронами и полем фазовая скорость волны υ_ф  должна примерно равняться скорости электронов и, следовательно, должна быть меньше скорости света в вакууме  с. Такие волны, у которых υ_ф < с, называются замедленными, а линии передачи, которые обеспечивают замедление фазовой скорости волны, называют замедляющими системами.

Замедляющие системы применяются не только в электронных приборах для усиления и генерирования колебаний, но и в линейных ускорителях заряженных частиц, в качестве линий задержки, в антенной технике.

Замедление волн можно осуществить двумя способами. Первый способ состоит в заполнении части пространства, где распространяется волна, диэлектриком с относительной диэлектрической проницаемостью, большей единицы. Возможность замедления волн при этом следует непосредственно из решения волновых уравнений, описывающих электромагнитное поле. Примером таких систем может служить диэлектрический волновод или металлический волновод, частично заполненный диэлектриком.

В приборах СВЧ такие системы практически не применяются, так как известные диэлектрики, обладающие малыми потерями, имеют небольшое значение диэлектрической проницаемости и поэтому не позволяют получить необходимое замедление волны. Кроме того,  их изготовление связано с определенными технологическими трудностями.

Другой способ замедления волн заключается в использовании специальных линий передач с периодической структурой. В таких линиях гладкие стенки, регулярные вдоль направления распространения волны, заменяются поверхностями сложной формы с периодическими граничными условиями. При этом волна, распространяясь вдоль поверхности сложной формы со скоростью света, следуя за её изгибами, будет иметь фазовую скорость в направлении оси системы меньшую скорости света. Именно такие линии передач с периодической структурой, получившие название периодических замедляющих систем, будут рассматриваться в настоящем пособии.

Для более глубокого изучения свойств замедляющих систем приводится библиографический список.

1. Общие свойства замедляющих систем

          Основным свойством замедляющих систем, как уже было сказано, является распространение волн с фазовыми скоростями меньше скорости света. Соответственно, основным параметром замедляющей системы является коэффициент замедления n  или просто замедление – отношение скорости света в вакууме к фазовой скорости волны:

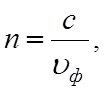
             > 1.                                             (1.1)                              

        Замедление можно выразить также через волновые числа в системе и в свободном пространстве, β и κ соответственно.

          Так как 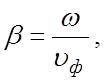     а 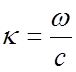 ,   ω – круговая частота поля, то

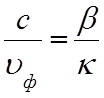    .                                                   (1.2)

Кроме того, поскольку 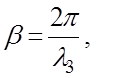а 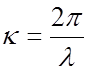, где λ₃, λ – длины волн в замедляющей системе (длина замедленной волны) и свободном пространстве, то

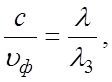                                                                             (1.3)

причем, при условии замедления волны

                                               β > κ ;  λ > λ₃ .                                                                         (1.4)

          Независимо от конструкции замедляющих систем им свойственны некоторые общие особенности, вытекающие из решения волновых уравнений для векторов электромагнитного поля при выполнении неравенств (1.1) и (1.4).

          Рассмотрим, в частности, особенности распределения поля в поперечном сечении замедляющих систем, отличающихся видом симметрии.

1.1.  Распределение поля в замедляющих системах

с плоскими границами

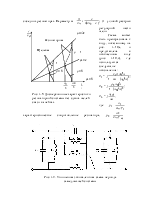
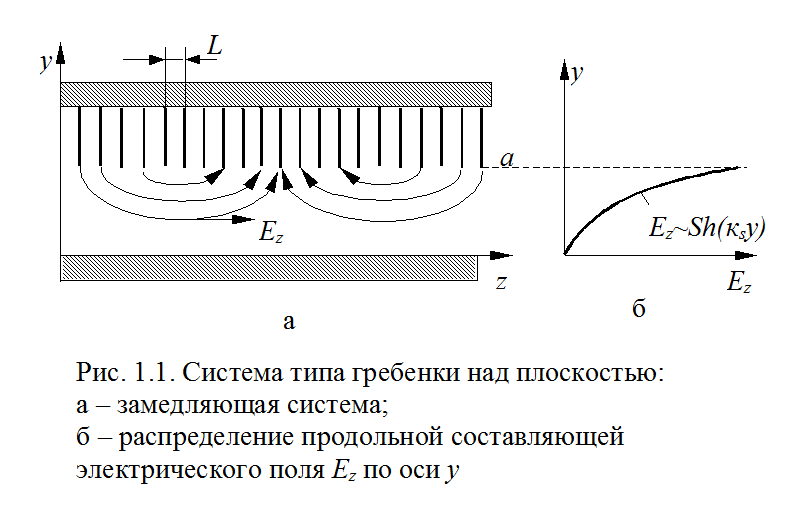
          Рассмотрим в качестве примера систему типа гребенки над плоскостью (рис.1.1). Система состоит из двух параллельных металлических пластин. В верхней пластине прорезаны пазы, образующие вместе с выступами гребенку. В области между гребенкой и нижней пластиной       0 < y <  вдоль оси z распространяется замедленная волна Е типа. В направлении оси x гребенка не ограничена, так что поле вдоль этой оси не меняется .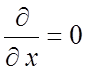 

Период системы L и толщину выступов полагаем малыми по сравнению с длиной замедленной волны. Благодаря этому требованию все составляющие поля изменяются вдоль оси  z, как в гладкой линии передач, по гармоническому закону e^jβz.  Условно такие системы относят к однородным.

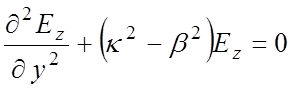                                          .                                  (1.5)

Решение (1.5) ищем для бегущих волн, для которых изменение полей в направлении оси z, как в однородных линиях описывается множителем

                                                   e^{j (ωt - βz)} .                                                                         (1.6)

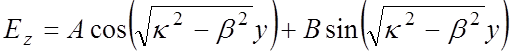 ,                        (1.7)

где A и В – некоторые постоянные; множитель (1.6) опущен.

Но из (1.4) следует, что подкоренное выражение κ² – β²  < 0. Введем обозначение

,                                                            (1.8)

подставим в (1.7) и получим

.