Замедляющие системы (основные свойства, характеристики, теоретические и экспериментальные методы исследования замедляющих систем): Учебное пособие, страница 12

и определяет эффективность взаимодействия электронного пучка с р-й пространственной гармоникой. В формуле  (5.5) величины 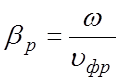 и υ_гр можно определить по дисперсионной характеристике, как показано в разделе 3, в точке пересечения касательной к дисперсионной характеристике с осью ординат (см. рис. 3.3). Относительные амплитуды гармоник А_р зависят от геометрии замедляющей системы и определяются по распределению продольной составляющей электрического поля в зазоре системы тем же способом, что и коэффициенты ряда Фурье. В случае толстых диафрагм, когда распределение поля Е_Z можно принять постоянным вдоль зазора d, коэффициенты А_р с достаточно большой точностью определяются соотношением

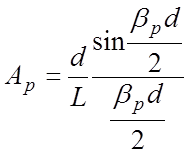.                                            (5.6)

          Для определения отношен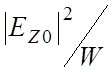ияиспользуется метод малых возмущений. В соответствии с теоремой малых возмущений величина отношения 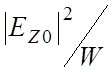связана с изменением резонансной частоты резонатора при внесении в него возмущающего тела соотношением

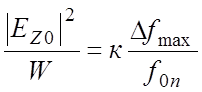,                                          (5.7)

где Δf_max – уход резонансной частоты на виде колебаний n при введении возмущающего тела в максимум электрического поля системы, f_0n – невозмущенная резонансная частота на n-м виде колебаний; к – постоянная возмущающего тела, зависящая от его формы, размеров и материала.

          Определение постоянной к производится путем калибровки возмущающего тела. Для этого тело помещают в калибровочный эталонный резонатор, возбуждаемый на резонансной частоте, близкой к резонансной частоте f_0nЗС, на которой измеряется сопротивление связи. Обычно для этой цели используется цилиндрический резонатор, возбуждаемый на виде колебаний Е₀₁₀, структура поля в котором известна и для которого, следовательно, отношение 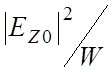может быть вычислено аналитически. Опуская промежуточные преобразования, можно получить следующую формулу для расчета калибровочного коэффициента к

,                                        (5.8)

где l, R – длина и радиус цилиндрического эталонного резонатора, см; Δf_э – изменение резонансной частоты резонатора при введении в него возмущающего тела вдоль оси, Мгц. Поскольку электрическое поле на оси цилиндрического резонатора на виде Е₀₁₀ однородно, то от глубины погружения тела в резонатор смещение частоты не зависит.

          Найденная таким образом калибровочная постоянная подставляется в формулы (5.7) и (5.5). Причем для каждого вида колебаний одновременно определяется сопротивление связи для любой р-й гармоники подстановкой значений А_р и β_р.

           Точность измерения сопротивления связи определяется точностью измерения смещения резонансной частоты исследуемого отрезка системы при введении возмущающего тела. При уменьшении объема тела искажения поля в исследуемом резонаторе уменьшаются, но повышаются требования к точности измерения малых сдвигов резонансной частоты. Достаточно высокую точность измерения частоты обеспечивает электронно-счетный частотомер.

5.4. Измерение холодных потерь

Методики измерения холодных потерь хорошо разработаны применительно к измерению затухания в волноводах и резонаторах. Одна из них заключается в измерении мощностей Р₁ и Р₂ бегущей волны на входе и выходе замедляющей системы. При этом ЗС должна быть хорошо согласована с генератором и нагрузкой. По отношению мощностей Р₁ и Р₂ можно оценить величину холодных потерь в замедляющей системе

  С = 10lg Р₁/Р₂, дБ                                        (5.9)

и постоянную затухания на единицу длины замедляющей системы:

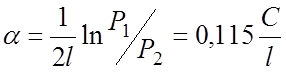,                               (5.10)

где l – длина замедляющей системы.

          Основная погрешность метода связана с потерями, обусловленными рассогласованием на входе и выходе системы. Для измерения на бегущей волне используют также метод замещения с помощью точного переменного аттенюатора.

          Для измерения потерь в макетах замедляющих систем применяются также резонансные методы, основанные на измерении добротности резонансного отрезка, закороченного на торцах системы.

В соответствии с определением добротности и с учетом того, что стоячая волна является суммой двух бегущих навстречу волн, потери энергии в резонаторе длиной l  можно выразить соотношением

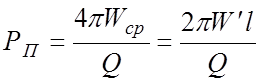,                                  (5.11)

где W_ср – полная запасенная энергия стоячей волны в резонаторе, W΄– запас энергии на единицу длины для каждой из бегущих волн.

          Обычно потери энергии в ЗС невелики, поэтому скорость распространения энергии в системе можно считать равной групповой скорости. В этом случае потери энергии на единицу длины резонатора за период колебаний равны

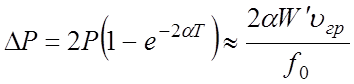,                               (5.12)

где Т и f₀ – период и частота резонансных колебаний, Р – мощность, переносимая бегущей волной.

          Следовательно, потери энергии в резонаторе длиной l за период резонансных колебаний равны

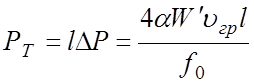.                                   (5.13)

Из сравнения выражений (5.11) и (5.13) следует, что постоянная затухания бегущей волны на единицу длины замедляющей системы

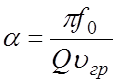.                                            (5.14)

          Потери в ЗС, выраженные в дБ, согласно (5.10) и (5.14) принимают вид

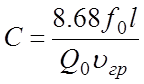, дБ.                                  (5.15)

          Таким образом, по измеренной величине добротности закороченного отрезка ЗС можно определить постоянную затухания α и величину полных потерь в замедляющей системе любой длины.

          Величину υ_гр в формулах (5.14), (5.15) определяют по дисперсионной характеристике системы. Измеряя Q для нескольких резонансных частот отрезка системы, можно найти зависимость коэффициента затухания в полосе пропускания всей системы.

Заключение