Замедляющие системы (основные свойства, характеристики, теоретические и экспериментальные методы исследования замедляющих систем): Учебное пособие, страница 11

Коэффициент замедления  согласно (1.3) оказывается равным: .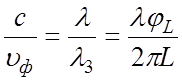

Изменяя частоту генератора и повторяя описанные выше измерения, можно получить зависимость замедления в полосе пропускания замедляющей системы, то есть дисперсионную характеристику. Следует, однако, отметить, что измерения в режиме бегущей волны не обеспечивают высокой точности. Большие погрешности возникают из-за рассогласования замедляющей системы с внешними цепями и появления вследствие этого нежелательных видов колебаний в исследуемом макете в полосе пропускания.

5.2.2. Резонансный метод

определения дисперсионных характеристик

При резонансном методе определения дисперсионных характеристик обычно используют отрезок ЗС, состоящий из 6-12 периодов системы. На торцах системы обеспечивается, как правило, режим холостого хода. Концами системы считаются плоскости симметрии крайних ячеек – электрические стенки, расположенные в плоскостях Z = const, на которых выполняются условия равенства нулю тангенциальной составляющей электрического поля, .

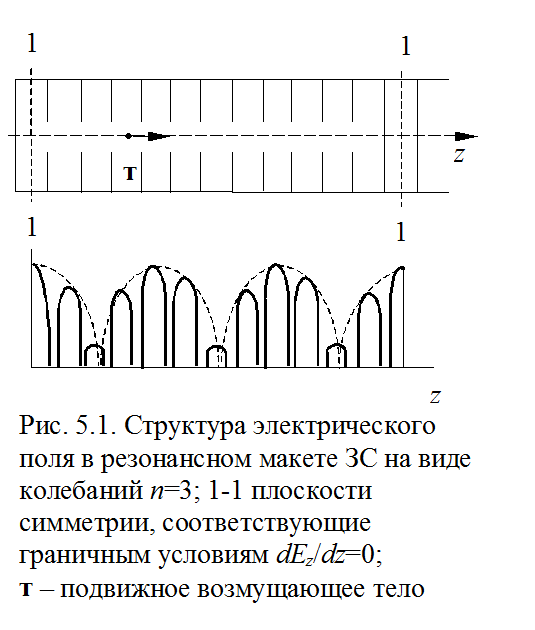
Сказанное поясняется рис. 5.1, на котором изображен отрезок ЗС длиной l, содержащий 13 периодов. Плоскости 1-1 обеспечивают холостой ход на концах отрезка. В макете предусмотрено перемещение возму-щающего тела т вдоль оси системы.

При резонансных измерениях отрезок замедляющей системы представляет объемный резонатор с достаточно высокой добротностью. В таком  резонансном  отрезке  линии при  резонансе между плоскостями 1-1 укладывается целое число замедленных полуволн любой гармоники поля.

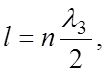                                               (5.1)

откуда следует 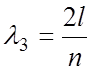, где n – число полуволн (обычно нулевой гармоники), укладывающееся на длине l, или номер вида колебаний. В макете может возбуждаться N+ 1 вид колебаний, где N – число периодов, которое размещается между плоскостями зеркальной симметрии, являющимися, как было указано выше, плоскостями холостого хода.

          Каждому виду колебаний соответствуют сдвиги фаз на период системы, определяемые также из условия резонанса:

 откуда 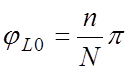.                          (5.2)

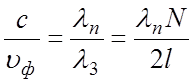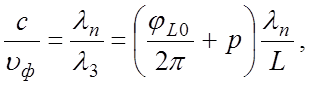С учетом (5.1) и (5.2) замедление можно определить по формуле     или                                    (5.3)

где  λ_n – резонансная длина волны на виде колебаний n.

          С учетом (5.2) получаем

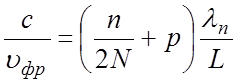.                                     (5.4)

          Следует отметить еще раз, что условие резонанса выполняется не только для нулевой, но и для любой пространственной гармоники.

          Практически настройка на резонансную частоту вида колебаний n осуществляется  по максимальному отклонению стрелки индикаторного прибора, на который сигнал подается с детектора, связанного с петлей в резонаторе. Определение значения n и соответствующей ему замедленной длины волны осуществляется по картине распределения электрического поля вдоль оси резонансного макета. Для этой цели используется метод малых возмущений. В соответствии с теоремой о малых возмущениях при перемещении возмущающего тела вдоль оси макета происходит изменение его резонансной частоты, пропорциональное квадрату напряженности электрического поля в месте расположения тела. В качестве возмущающего или пробного тела обычно используется небольшая металлическая или диэлектрическая бусинка, имеющая достаточно малые размеры, чтобы структура поля в исследуемом резонаторе практически не изменялась при её перемещении и в то же время изменение резонансной частоты было достаточным, чтобы его можно было измерить.

          Расстройка резонатора относительно частоты генератора приводит к уменьшению амплитуды колебаний в резонаторе. Таким образом, сигнал с детектора, фиксирующего амплитуду поля в резонаторе, оказывается тем меньше, чем больше напряженность поля в точке, где находится возмущающее тело и, следовательно, больше расстройка частоты.

          Картину распределения поля в ЗС можно получить, перемещая возмущающее тело вдоль ее оси. При этом каждому виду колебаний n на резонансной частоте f_n соответствует определенная картина распределения электрического поля вдоль макета, которая и позволяет идентифицировать данный вид колебаний. В качестве примера на рис. 5.1 приведена картина распределения электрического поля вдоль отрезка замедляющей системы, соответствующая виду колебаний n = 3. Картина получена с помощью самописца.

          При изменении частоты генератора сдвиг фаз между  ячейками системы меняется от 0 до π и в резонаторе возбуждаются виды колебаний согласно условию (5.2) n= 0, 1, 2…N. То есть полное число резонансов равно N+1.  Соответственно число дискретных отсчетных точек, по которым строится дисперсионная характеристика, возрастает с увеличением числа N периодов в макете. Кроме того, при увеличении N уменьшается влияние искажения поля у торцевых плоскостей. Однако при этом затрудняется определение порядкового номера вида колебаний по распределению поля вдоль оси отрезка. По измеренным с помощью частотомера резонансным частотам и соответствующим им номерам видов колебаний строятся дисперсионные характеристики по (5.4) согласно методике, описанной в разделе 3.2.

          Следует отметить, что при данном способе определения дисперсионных характеристик измерения производятся в отдельных, дискретных точках, соответствующих условиям резонанса. Поэтому для построения характеристики ее приходится экстраполировать между измеренными точками гладкой кривой.

5.3.  Измерение сопротивления связи

Как было показано в разделе 3.3, сопротивление связи для р-й гармоники выражается формулой

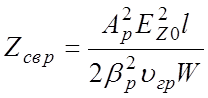                                          (5.5)