Замедляющие системы (основные свойства, характеристики, теоретические и экспериментальные методы исследования замедляющих систем): Учебное пособие, страница 8

,                                              .

Здесь и далее поля в области I обозначены одним штрихом, а в области II – двумя штрихами. Кроме того, напомним что согласно (1.10) поперечное волновое число 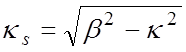. Распределение продольной составляющей Е_z по радиальной координате показано на рис.4.2,г. Поперечные составляющие, как и для регулярных волноводов, можно выразить через продольные составляющие полей и получить окончательно:

в области I (r ≤ ):                                        в области II (r ≥ ):

                                                         

                                                

                                            

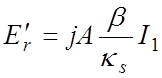
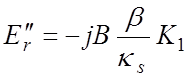
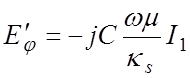
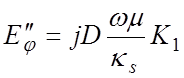
                                                                                       (4.9)

                                              

                                            .

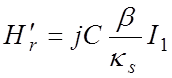
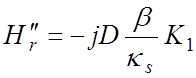
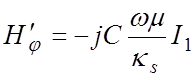
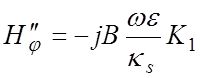В этих выражениях I₁  , K₁ – модифицированные функции Бесселя первого и второго рода первого порядка. Аргумент κ_sr  у всех функций опущен для краткости записи.

          Используем граничные условия для определения постоянных и для «сшивания» полей на границе двух областей r = . Составляющие поля Е_z и Е_φ, касательные к проводящей поверхности на границе двух областей, непрерывны, т. е.  и , откуда следует:

,                                               (4.10)

                                                   .                                              (4.11)  Здесь и далее аргумент     κ_s у функций Бесселя опущен.

          В направлении протекания тока в спирально проводящем цилиндре под углом ψ к оси электрическое поле должно обращаться в ноль из-за бесконечно большой проводимости:

 или

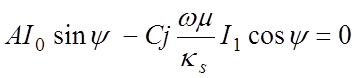   .                                 (4.12)

          Составляющие магнитного поля, касательные  к  цилиндру в направлении  угла ψ, также должны быть непрерывны, так  как  в перпендикулярном к нему направлению токов нет.  и, следовательно,

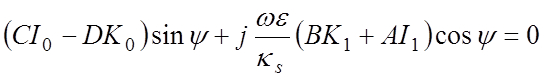.                    (4.13)

В уравнениях (4.10) – (4.12) три коэффициента можно выразить через четвертый:

.

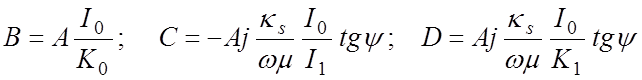Подставим их в (4.13) и после преобразований получим уравнение, в котором отсутствуют произвольные постоянные

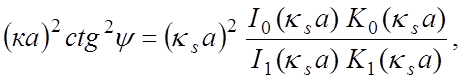                      (4.14)

где .

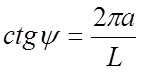          Уравнение (4.14) является дисперсионным уравнением неэкранированной спирали. Оно устанавливает связь между текущим волновым числом к и поперечным волновым числом к_s и, следовательно, фазовой постоянной 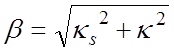. При этом замедление может быть определено как .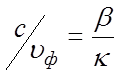

          Проанализируем полученное уравнение. С ростом частоты и, следовательно, 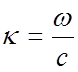, постоянная к_s также растет и отношение в правой части уравнения стремится к единице 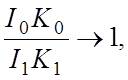 откуда:

 

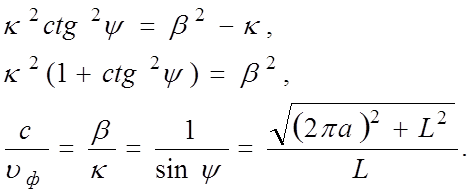
Таким образом, на высоких частотах мы получили такой же результат (4.7), который имели, исходя из простейших соображений: волна распространяется вдоль витков спирали со скоростью света.

          На низких частотах поле занимает больший объем вокруг спирали, и спираль мало влияет на скорость волны. Она распространяется в этом случае подобно поперечной волне вдоль гладкого цилиндра, заменяющего собой спираль, а замедление равно единице.

          При построении дисперсионной характеристики спирали часто по оси абсцисс откладывают приведенный параметр к_s. При этом дисперсионные зависимости становятся универсаль-ными для различных спиральных ЗС. Пример таких дисперсионных характеристик приведен на рис. 4.3. Можно заметить, что наибольшая дисперсия в спирали наблюдается в области низких частот, когда к_s < 1,2. Поэтому спирали, предназначенные для широкополосных приборов, обычно работают на частотах, когда    к_s > 1,2.

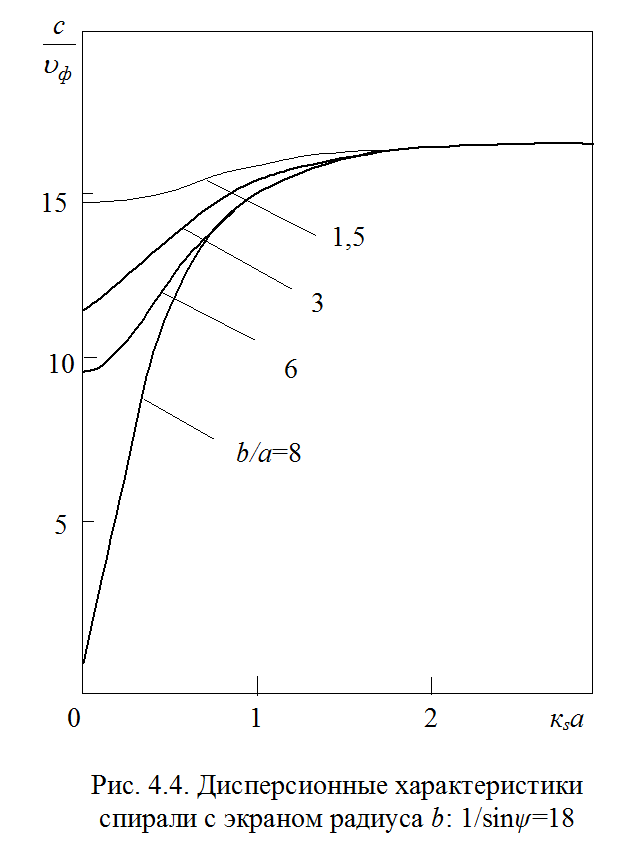          Проводящий экран, в который обычно помещают спираль, влияет на дисперсионную хара-ктеристику в области низких частот, умень-шая дисперсию (рис. 4.4). Объясняется это тем, что при наличии экрана большая часть энергии поля оказывается сосредоточенной вблизи спирали не только на высоких, но и на низких частотах.

4.2.2. Сопротивление

связи спиральной ЗС

Для определения сопротивления связи по формуле (3.13) необходимо определить мощность , переносимую волной, согласно (3.13). При этом следует интегрировать отдельно по внутренней и внешней областям спирали.

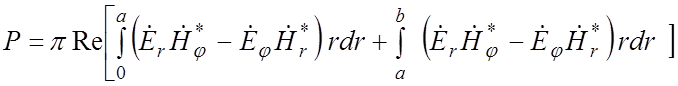,           (4.15)

где – комплексные амплитуды составляющих электрического поля;  – комплексно-сопряженные амплитуды составляющих магнитного поля.

Как показано в [6], полученное в результате интегрирования (4.15) громоздкое выражение, содержащее модифицированные функции Бесселя первого и второго рода, нулевого и первого порядка, можно для сопротивления на оси спирали аппроксимировать приближенным выражением

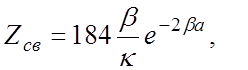Ом.

Расчеты показывают, что сопротивление связи спирали быстро уменьшается с ростом частоты. Объясняется это, в частности, тем, что с увеличением частоты и, следовательно, к_s  поле быстрее убывает при удалении от витков спирали. По этой причине применение спирали в электронных приборах ограничивается в области высоких частот, при которых значение  к_s  > 2,2.

4.3.  Диафрагмированный круглый волновод

Диафрагмированный круглый волновод с обозначением размеров показан на рис. 2.3,в. Подобные ЗС применяются в основном в линейных ускорителях заряженных частиц и реже – в лампах бегущей волны.

          Проведем анализ системы, используя метод сшивания полей в частичных областях I –  и II –  на границе .

          Для цилиндрической области I поле, обладающее осевой симметрией 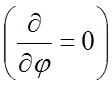, можно представить в виде суммы пространственных гармоник основного типа волны Е₀₁ в круглом волноводе. При условии замедления составляющие электромагнитного поля, как следует из (3.5) и (4.9), имеют вид:

,

,

.

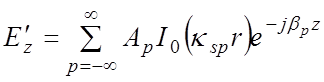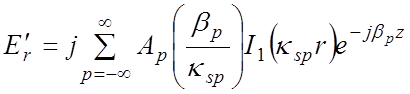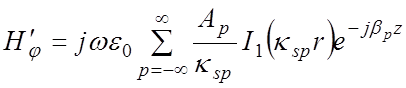          Постоянные А_р характеризуют интенсивность гармоники каждой составляющей поля и могут быть определены из условия непрерывности E_z при .

          Остальные составляющие поля в области I при условии осевой симметрии отсутствуют.