Кроме того, все дисперсионные характеристики заключены в интервале λπ/L и λ0/L, определяемом границами полосы пропускания системы. Эти границы показаны на рис. 3.3 в виде соответствующих вертикальных линий. На рис. 3.2,б этим границам соответствуют значения κπ и κ0. Приведенные на рис. 3.3 дисперсионные характеристики изображены для случая λ0 > λπ. Нулевая гармоника имеет при этом положительную и нормальную дисперсию.
Для
определения групповой скорости достаточно провести касательную к дисперсионной
характеристике любой гармоники на заданной длине волны (частоте) до пересечения
с осью ординат с/υф. Все касательные пересекут эту ось в
одной точке, соответствующей величине с/υгр на данной
частоте. Действительно, как следует из рис. 3.3, величина ОС = АВ
+ВD=
=
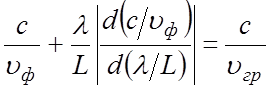, что соответствует уравнению (3.9).
Как было сказано выше, если ЗС полностью экранирована, то граничные
длины волн имеют конечные значения, а на границах полосы пропускания мощность,
передаваемая по линии, и, следовательно, υгр
равны нулю. Такое явление наблюдается и в регулярных волноводах на критической
частоте. При этом касательная к дисперсионной характеристике оказывается
параллельной оси ординат и нигде её не пересекает, что и соответствует υгр= 0.
По этой причине все дисперсионные характеристики вблизи границ полосы
пропускания имеют характерные изгибы, так что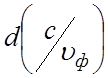 
/
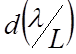= ∞ при λ = λ0
и λ = λπ.
Отметим также, что для создания более компактных графиков дисперсионные характеристики отрицательных гармоник часто изображают в положительной полуплоскости, как показано на рис. 3.3 штриховыми линиями. При этом на границах полосы пропускания дисперсионные характеристики положительных и отрицательных гармоник попарно соединяются. Действительно, как следует из (3.11), на верхней границе коэффициенты замедления для положительных и отрицательных гармоник с одинаковыми номерами одинаковы с точностью до знака. На нижней границе будут одинаковы по абсолютной величине коэффициенты замедления положительной гармоники с номером р и отрицательной – с номером р + 1.
3.3. Сопротивление связи
Для замедляющих систем, используемых в электронных приборах, большое значение имеет параметр, определяющий эффективность взаимодействия электронов с продольной составляющей электрического поля волны. Таким параметром является сопротивление связи Zcв, которое связывает напряженность электрического поля Еz с мощностью, переносимой волной Р. Сопротивление связи можно по аналогии с эквивалентным сопротивлением волновода определить как отношение
,
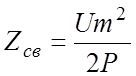(3.12)
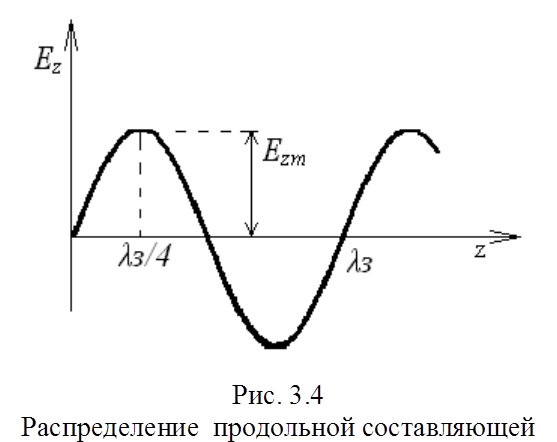
где Um – амплитуда напряжения бегущей волны, рассчитанная в продольном направлении, Р – мощность, переносимая волной. Амплитуда Um определяется между точками ЗС, отстоящими вдоль оси z на расстоянии, равном λ3/4, то есть от точки с нулевой напряженностью поля Еz до максимальной напряженности, как показано на рис. 3.4.
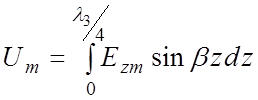. Так как 
,
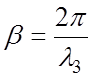то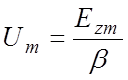 
.
Следовательно,
.
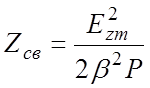(3.13)
Мощность Р определяется как поток вектора Умова-Пойнтинга через поперечное сечение S замедляющей системы.
,
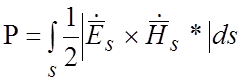(3.14)
 |
- комплексные
векторные амплитуды поперечных составляющих электрического и магнитного
(комплексно-сопряженая амплитуда) полей бегущей волны. Мощность Р может
быть выражена через энергию W1,
содержащуюся в электромагнитном поле на единице длины линии, и групповую
скорость (скорость переноса энергии P = W1υгр.
Тогда (3.13) принимает вид
.
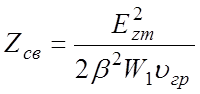(3.15)
В случае неоднородных систем, когда поле представляется суммой пространственных гармоник с амплитудами Еzp и фазовыми постоянными βр, каждая гармоника характеризуется своим сопротивлением связи
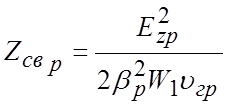. (3.16)
Как следует из (3.16), сопротивление связи тем больше, чем меньше групповая скорость и, согласно (3.9), чем больше дисперсия.
Поскольку Еz является функцией поперечных координат, то величина Zсв зависит от места его определения. Наибольшее значение оно имеет вблизи неоднородностей ЗС и уменьшается при удалении от них из-за уменьшения поля Еz .
Для ряда ЗС расчет сопротивления связи представляет трудную задачу, поэтому часто его величину определяют экспериментально.
4. Характеристики некоторых типов замедляющих систем
4.1. Методы анализа замедляющих систем
4.1.1. Полевые методы
Анализ замедляющих систем сводится, прежде всего, к выводу дисперсионных уравнений, которые связывают геометрические размеры, частоту (длину волны) колебаний с фазовой скоростью (замедлением) волны, и определению сопротивления связи. Наиболее полную и достоверную информацию о характеристиках и параметрах замедляющих систем позволяют получить электродинамические методы решения полевых задач, которые в конечном счете сводятся к решению уравнений электромагнитного поля при граничных условиях, заданных геометрией системы.
Однако аналитическое решение этих уравнений в большинстве случаев возможно только для двумерных систем с простой конфигурацией границ, например, совпадающих с координатными поверхностями. В основе решения уравнений при этом обычно лежит метод сшивания полей на границах частичных областей системы. Получаемые в результате такого подхода дисперсионные уравнения довольно громоздки, и расчет по этим уравнениям часто представляет трудоемкую задачу.
Для систем с более сложной геометрией используют численные методы решения волновых уравнений с применением высокопроизводительных ЭВМ. Эти методы иногда применяют и для трехмерных замедляющих
систем. Применение метода частичных областей для получения дисперсионных уравнений проиллюстрировано ниже на примере спиральной ЗС и диафрагмированного круглого волновода.
4.1.2. Метод эквивалентных схем
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.