Замедляющие системы (основные свойства, характеристики, теоретические и экспериментальные методы исследования замедляющих систем): Учебное пособие, страница 5

          Процесс распространения волны в периодической структуре можно рассматривать как процесс последовательного её отражения от неоднородностей. Если сдвиг фазы волны на период структуры равен  0 или π,  то волны, отраженные от всех неоднородностей, оказываются в фазе, в результате чего волна полностью отражается и распространение её в ЗС становится невозможным. Этот факт далее доказывается на основе метода эквивалентных схем. Двум значениям φ_L0, равным 0 и π, соответствуют две граничные частоты ω₀ и ω_π (длины волны λ₀ и λ_π). Следовательно, замедляющие системы имеют некоторую полосу пропускания, причем для некоторых систем одна из граничных частот может принимать значение 0 или бесконечность. В полностью экранированных системах эти частоты обычно имеют конечное значение.

          В полосе пропускания фазовый сдвиг φ_L0 плавно меняется от 0 до π, а β₀ – от 0 до π/L. Для гармоники с номером р фазовый сдвиг в полосе частот заключен между значениями , а фазовая постоянная 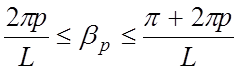 для неотрицательных р. Для отрицательных р знак неравенства меняется на противоположный.

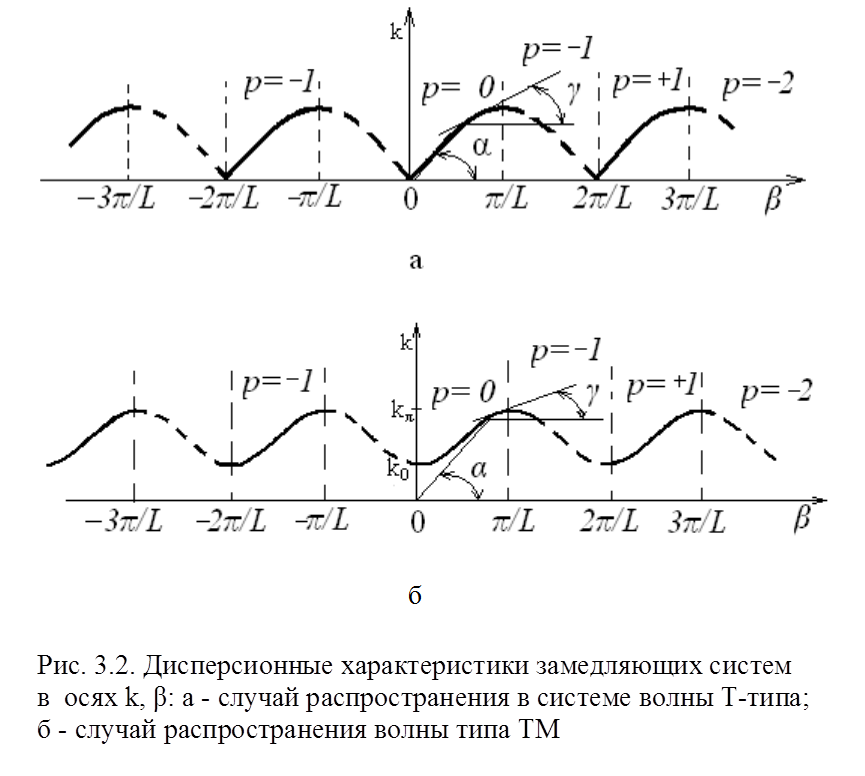
          Пример дисперсионных характеристик в виде зависимостей               κ = κ ( β)  приведен на рис. 3.2.

  

          На рис. 3.2,а. качественно изображен график κ = κ ( β ) для замедляющей системы, в которой между неоднородностями распространяется волна Т типа (поперечная волна). Примером подобной системы является гребенка над проводящей поверхностью (рис. 1.1), но с периодом и толщиной выступов, соизмеримыми с длиной волны. Согласно (3.6) 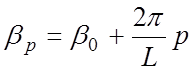и при р=0 фазовая постоянная β_р равна β_р=2πр/L. Поэтому, кроме точки к=0, β=0, существует бесконечный ряд значений β_р, соответствующих различным р и лежащих вдоль оси абсцисс на одинаковых расстояниях, равных 2π/L. По мере повышения частоты постоянные к и β₀ увеличиваются. На некоторой частоте фазовый сдвиг β₀L становится равным π, что приводит к синфазному сложению отраженных от неоднородностей волн, и передача энергии по линии прекращается. Групповая скорость при этом оказывается равной нулю, что справедливо для всех гармоник, так как при этом β_р=π/L+2πр/L.

          Таким образом, зависимости κ = κ ( β ) представляют периодические функции с четной симметрией. С их помощью можно определить замедление фазовой и групповой скорости любой гармоники. Так как 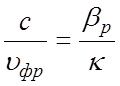, а 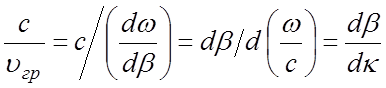 , то замедление фазовой скорости равно  ctg α, а замедление групповой  скорости  равно ctg γ. Для р = 0 ctg α и  ctg γ имеют одинаковые знаки, а для р = –1 – разные. Значения ctg α для данной частоты (к = const) растут с увеличением р, а ctg γ остаются постоянными.

Из сказанного выше следует, что дисперсионная кривая  κ = κ ( β ) имеет бесчисленное множество максимумов при значениях β_р, лежащих посредине, между β_р=2πр/L β_р=2π(р+1)/L, когда υ_гр и соответственно ctg γ равны нулю.

Системы, у которых между неоднородностями распространяются ТЕ и ТМ волны, обладающие дисперсией, а волны Т типа отсутствуют, имеют дисперсионные характеристики, показанные на рис. 3.2,б. В данном случае системы обладают конечной полосой пропускания, ограниченной со стороны высоких и низких частот. На обеих границах полосы групповые скорости равны нулю и, следовательно, касательные к дисперсионным характеристикам в этой точке имеют нулевой наклон к оси абсцисс.

Рассмотрим теперь пример дисперсионных характеристик в осях 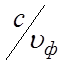, . Эти характеристики показаны на рис. 3.3 и могут быть получены с помощью зависимостей рис. 3.2,б, так как 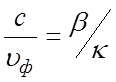, а .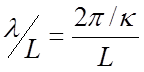

          Коэффициент замедления можно представить в виде зависимости от φ_L0 , так как 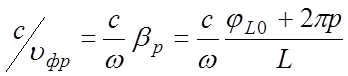. Выразив ω через длину волны λ , получим

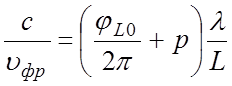,                                            (3.11)

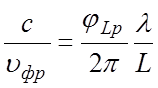                               или    .                                            (3.11а)

ностей волн, и передача энергии по линии прекращается. Групповая скорость при этом оказывается равной нулю, что справедливо для всех гармоник, так как при этом β_р=π/L+2πр/L.

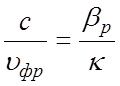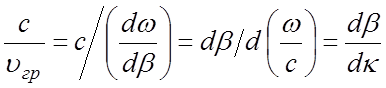          Таким образом, зависимости κ = κ ( β ) представляют периодические функции с четной симметрией. С их помощью можно определить замедление фазовой и групповой скорости любой гармоники. Так как , а  , то замедление фазовой скорости равно  ctg α, а замедление групповой  скорости  равно ctg γ. Для р = 0 ctg α и  ctg γ имеют одинаковые знаки, а для р = –1 – разные. Значения ctg α для данной частоты (к = const) растут с увеличением р, а ctg γ остаются постоянными.

Из сказанного выше следует, что дисперсионная кривая  κ = κ ( β ) имеет бесчисленное множество максимумов при значениях β_р, лежащих посредине, между β_р=2πр/L β_р=2π(р+1)/L, когда υ_гр и соответственно ctg γ равны нулю.

Системы, у которых между неоднородностями распространяются ТЕ и ТМ волны, обладающие дисперсией, а волны Т типа отсутствуют, имеют дисперсионные характеристики, показанные на рис. 3.2,б. В данном случае системы обладают конечной полосой пропускания, ограниченной со стороны высоких и низких частот. На обеих границах полосы групповые скорости равны нулю и, следовательно, касательные к дисперсионным характеристикам в этой точке имеют нулевой наклон к оси абсцисс.

Рассмотрим теперь пример дисперсионных характеристик в осях 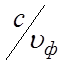, . Эти характеристики показаны на рис. 3.3 и могут быть получены с помощью зависимостей рис. 3.2,б, так как 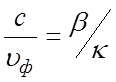, а .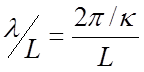

          Коэффициент замедления можно представить в виде зависимости от φ_L0 , так как 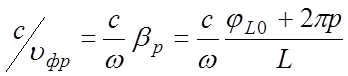. Выразив ω через длину волны λ , получим

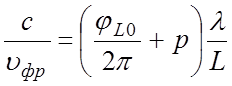,                                            (3.11)

                               или 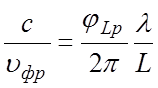   .                                            (3.11а)

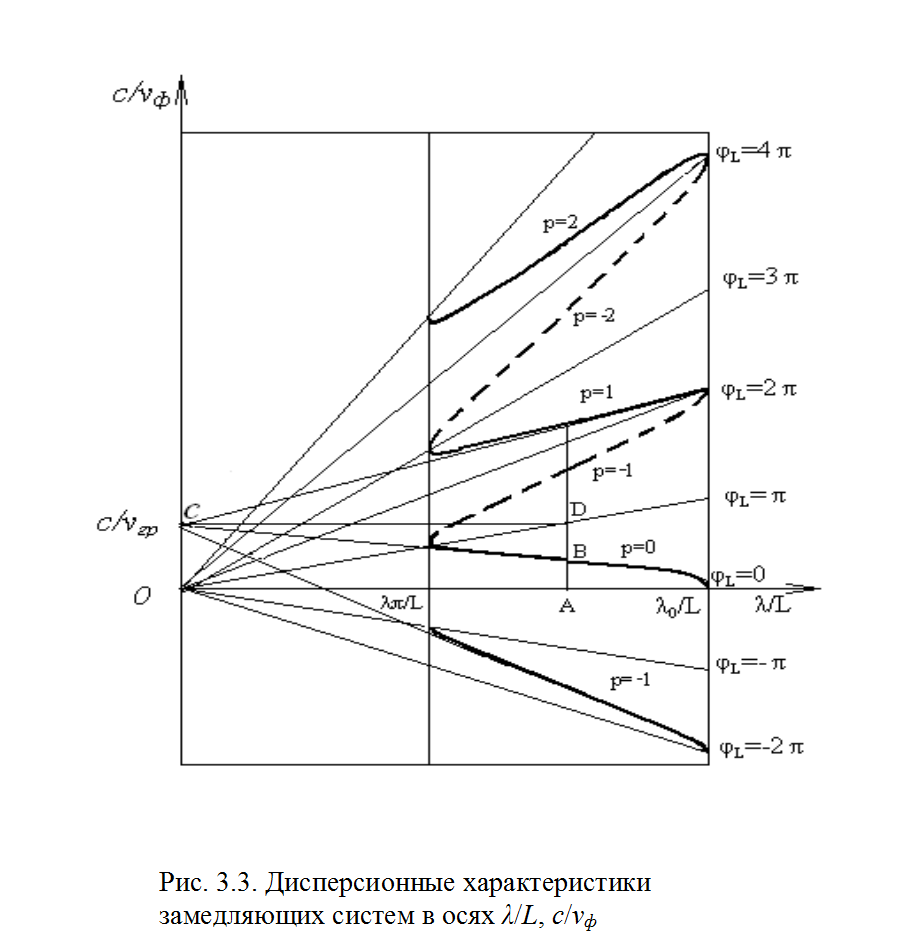          Из (3.11) следует, что замедление 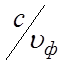при постоянном φ_L является линейной функцией . В результате дисперсионная характеристика для каждой гармоники оказывается заключенной между прямыми, исходящими из начала координат  и соответствующими значениям φ_L0 = 0 и φ_L0 = π. Эти прямые описываются уравнениям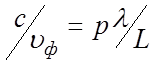и и 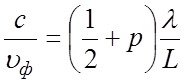 и изображены на рис. 3.3 в виде тонких линий φ_L = const. Дисперсионная характеристика основной гармоники (р = 0) располагается между линиями  φ_L = 0 и φ_L = π. Дисперсионные характеристики остальных гармоник соответственно располагаются между линиями φ_Lр = 2πр и φ_Lр = π (2р+1).