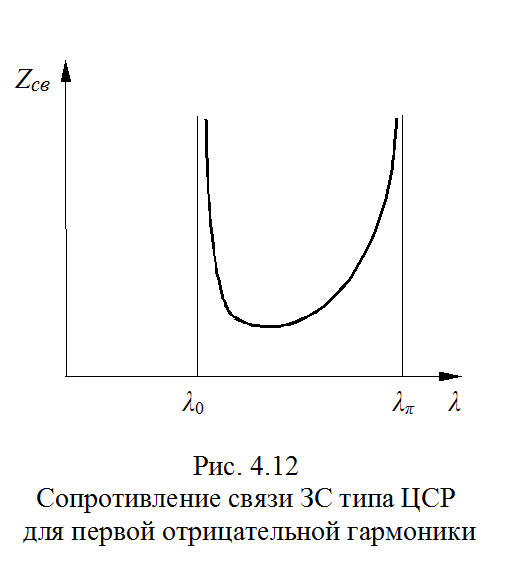
 На рис. 4.12 показана также типичная зависимость
сопротивления связи в основной полосе пропускания для гармоники р = –1.
На границах полосы пропускания сопротивление связи становится бесконечно большим,
так как групповая скорость и передаваемая мощность оказываются равными нулю.
На рис. 4.12 показана также типичная зависимость
сопротивления связи в основной полосе пропускания для гармоники р = –1.
На границах полосы пропускания сопротивление связи становится бесконечно большим,
так как групповая скорость и передаваемая мощность оказываются равными нулю.
4.5. Замедляющая система типа встречные штыри
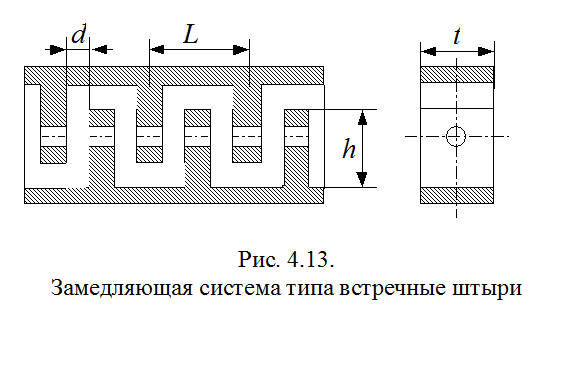 Пример системы типа встречные штыри показан на рис. 4.13.
Штыри могут быть образованы длинными тонкими или широкими стержнями длиной h.
В первом случае система используется для взаимодействия с ленточным электронным
потоком. Во втором случае в широких стрежнях имеются отверстия – пролетные
каналы для цилиндрического электронного луча. Пространственный период системы L
включает два зазора шириной d. Такую
систему можно рассматривать как многократно изогнутую линию, в которой волна
распространяется вдоль штырей в направлении оси y с фазовой
скоростью, равной скорости света с. Если система представляет
многократно изогнутый прямоугольный волновод, то следует учесть ди-сперсию
скорости волны в направлении оси у. Определим фазовую скорость
волны в направлении оси z. Изменение фазы волны на период системы для
произвольной гармоники с номером р равно
Пример системы типа встречные штыри показан на рис. 4.13.
Штыри могут быть образованы длинными тонкими или широкими стержнями длиной h.
В первом случае система используется для взаимодействия с ленточным электронным
потоком. Во втором случае в широких стрежнях имеются отверстия – пролетные
каналы для цилиндрического электронного луча. Пространственный период системы L
включает два зазора шириной d. Такую
систему можно рассматривать как многократно изогнутую линию, в которой волна
распространяется вдоль штырей в направлении оси y с фазовой
скоростью, равной скорости света с. Если система представляет
многократно изогнутый прямоугольный волновод, то следует учесть ди-сперсию
скорости волны в направлении оси у. Определим фазовую скорость
волны в направлении оси z. Изменение фазы волны на период системы для
произвольной гармоники с номером р равно
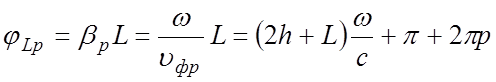 ,
(4.21)
,
(4.21)
где р = 0; ± 1, ± 2,….. – номер гармоники. Множитель 2h + L – средняя длина пути волны Т типа в линии, приходящейся на период структуры. Второе слагаемое в правой части (4.21) учитывает изменение фазы волны, обусловленное изгибом линии. Из (4.21) получаем формулу для замедления волны
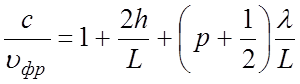 .
(4.22)
.
(4.22)
Замедление по групповой скорости
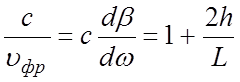 .
(4.23)
.
(4.23)
В
данном случае с/![]() не зависит от
частоты, что является следствием отсутствия дисперсии волны, распространяющейся
в направлении стержней.
не зависит от
частоты, что является следствием отсутствия дисперсии волны, распространяющейся
в направлении стержней.
Дисперсионные характеристики пространственных гармоник системы типа встречные штыри без экрана приведены на рис. 4.14.
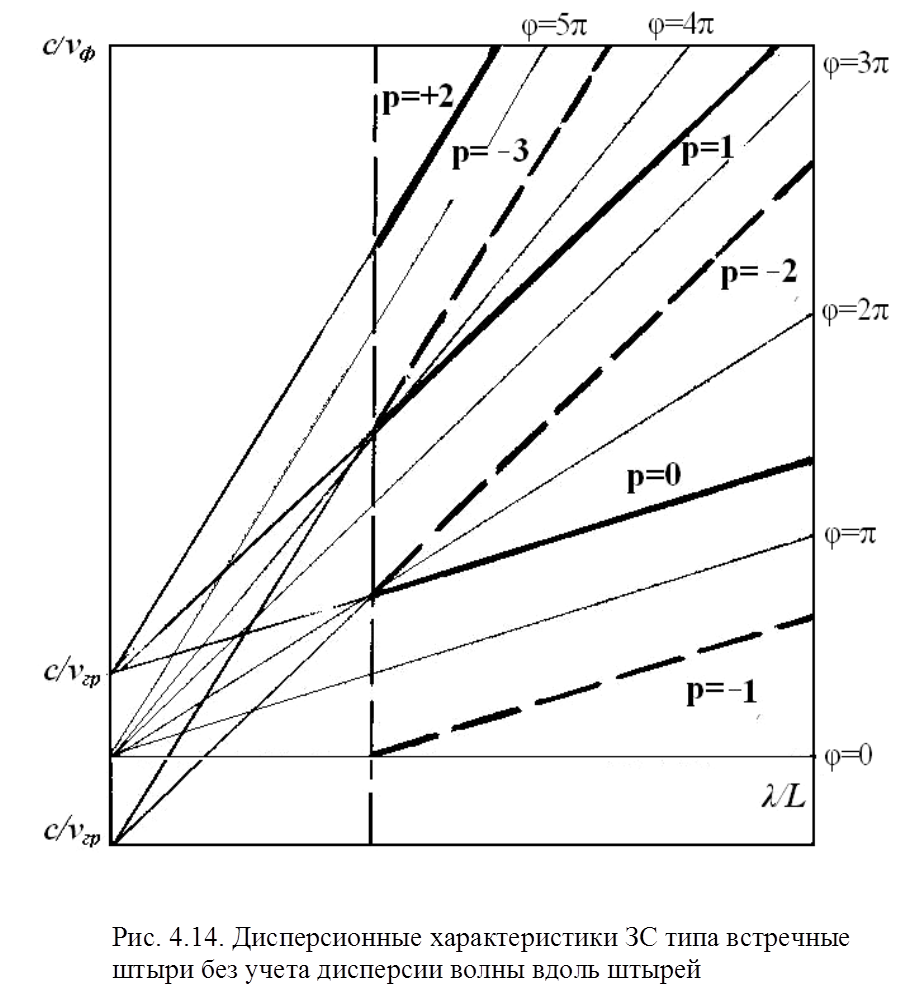 |
Отметим, что в рассматриваемом приближении коэффициент замедления для
любой гармоники является линейной функцией длины волны. Наименьшее замедление и
соответственно наибольшую фазовую скорость имеет первая отрицательная
гармоника, которая и считается основной. Границы полосы пропускания выбраны
условно по фазовому сдвигу первой отрицательной гармоники, изменяющемуся в
пределах ![]() .
.
При
этом рабочий диапазон длин волн оказывается заключенным в пределах ![]() .
.
Амплитуды гармоник зависят от координаты у. Так, в средней плоскости у = 0 амплитуды нулевой и четных гармоник оказываются равными нулю. При удалении от этой плоскости к стенкам амплитуды этих гармоник уже не равны нулю, причем поле каждой гармоники изменяется вдоль оси у различным образом.
Сопротивление связи рассматриваемой системы можно определить исходя из выражения (3.13) для р-й гармоники
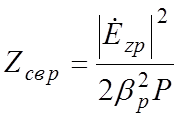 . (4.24)
. (4.24)
Полагая, что поле в зазоре d между штырями при у = 0 однородно, разложим его в ряд и определим амплитуды гармоник.
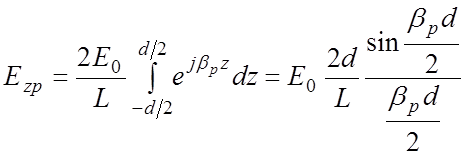 ,
(4.25)
,
(4.25)
где Е0 – напряженность поля в зазоре.
Мощность Р определяется, как для полосковой линии
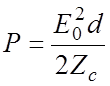 ,
(4.26)
,
(4.26)
где
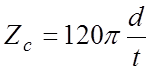 – волновое сопротивление полосковой линии, t
– ширина стержня.
– волновое сопротивление полосковой линии, t
– ширина стержня.
После подстановки (4.26) и (4.25) в (4.24) и преобразований получим
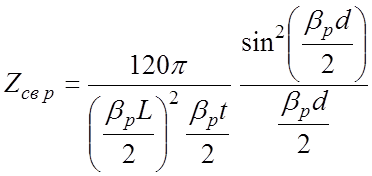 .
(4.27)
.
(4.27)
Анализ формулы (4.27) показывает, что для получения максимальной
величины Zсв необходимо выбирать
(βрd)опт ![]() 2,33.
Ширина штырей должна быть по возможности меньшей. Однако существуют
ограничения, обусловленные наличием пролетных каналов, проходящих через
середины стержней.
2,33.
Ширина штырей должна быть по возможности меньшей. Однако существуют
ограничения, обусловленные наличием пролетных каналов, проходящих через
середины стержней.
5. Экспериментальное определение параметров замедляющих систем
5.1. Общие замечания
Таким образом, холодные измерения параметров замедляющих систем являются часто необходимым этапом перед окончательной сборкой и горячими испытаниями прибора.
5.2. Экспериментальное определение
дисперсионных характеристик
5.2.1. Измерения в режиме бегущих волн
Измерения в режиме бегущих волн сводятся к измерению разности фаз
бегущей волны в двух точках замедляющей системы, расстояние между которыми
вдоль оси системы строго фиксировано. В системах с периодической структурой это
расстояние принимается равным или кратным периоду системы. Разность фаз в этих
двух точках обычно оценивается сравнением фазы бегущей волны в исследуемой
замедляющей системе с фазой волны в эталонной измерительной линии. Сдвиг фаз
волны φL на период системы определяется по разности отсчетов
на шкале расстояний измерительной эталонной линии для двух положений зонда в
этой линии, соответствующих минимальным показаниям индикаторного прибора. При
этом период Lи
сдвиг фаз φL определяют фазовую постоянную ![]()
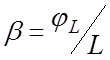 и длину замедленной волны
и длину замедленной волны 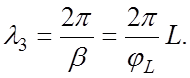
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.