Замедляющие системы (основные свойства, характеристики, теоретические и экспериментальные методы исследования замедляющих систем): Учебное пособие, страница 4

Распределение составляющих электромагнитного поля волны, распространяющейся вдоль замедляющей системы, существенно зависит от отношения периода системы к длине волны. Если это отношение много меньше единицы (период мал по сравнению с длиной волны), то поле в такой системе можно описывать одной бегущей волной с гармоническим распределением поля вдоль оси z. Эти ЗС принято с некоторым приближением считать однородными. К ним относятся, например структуры, приведенные на рис. 1.1 и рис. 1.2, а также спиральные ЗС, выполненные из тонкой проволоки и с малым шагом. Прочие периодические структуры, у которых период соизмерим с длиной волны, относят к неоднородным. Распределение поля в них вдоль оси z имеет более сложный характер.

          Рассмотрим в качестве примера систему типа гребенки в прямоугольном волноводе (рис 2.3,а). Причем период системы L и толщина выступов t соизмеримы с длиной замедленной волны. На рис. 3.1 показано распределение составляющей электрического поля Е_z вдоль системы при   . Амплитуда составляющей Е_z  является функцией не только поперечных координат х, у, как в регулярных линиях передач, но и функцией продольной координаты z. Причем в силу периодичности системы поле в каждой ячейке описывается одной и той же функцией, но отличается по фазе на одну и ту же величину. Следовательно,

 ,                                 (3.1)

где φ_L = βL – фазовый сдвиг волны на период системы, β – фазовая постоянная суммарного поля.

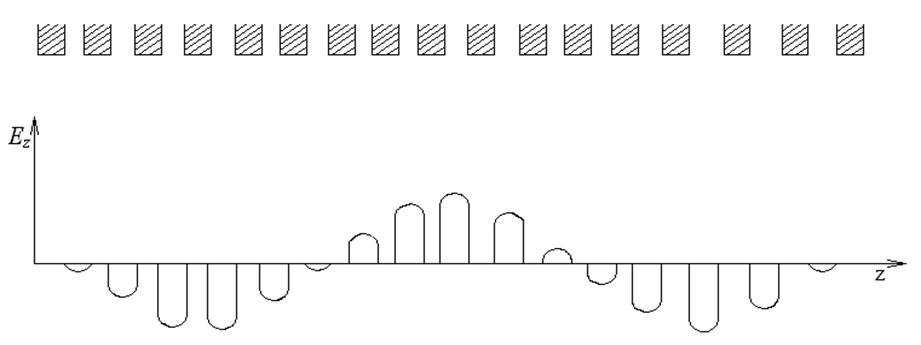
Рис. 3.1. Распределение составляющей электрического поля Е_zвдоль периодической  замедляющей системы

Равенство (3.1) отражает общие закономерности распространения волн в ЗС, которые определяются  теоремой Флоке: электромагнитное поле в поперечных сечениях ЗС, отстоящих друг от друга на период, отличаются только фазовым множителем φ_L.

          Таким образом, составляющие электромагнитного поля могут быть записаны в виде бегущей волны, амплитуда которой является произведением функции поперечных координат на периодическую функцию продольной координаты z.

,                                     (3.2)

где                                    ,                                (3.3)

комплексная амплитуда составляющей Е_z , F(z) – периодическая функция, зависящая от геометрии  ЗС.

          Функцию F(z) можно разложить в ряд гармонических составляющих – ряд Фурье, но не по временному, а по пространственному периоду L.

          В комплексной форме этот ряд записывается в виде

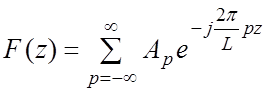  ,                                    (3.4) 

где А_р – коэффициенты разложения ряда Фурье, p = 0;   ± 1; ± 2; ….. номер члена разложения.

Коэффициенты А_р вычисляются по формуле

.

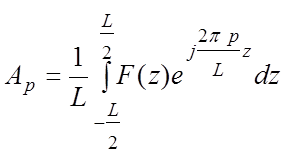Подставив (3.4) в (3.3) и (3.2) и внеся общие множители под знак суммы, получим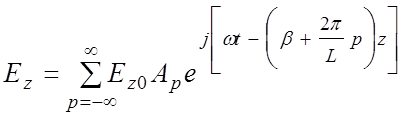                           

или 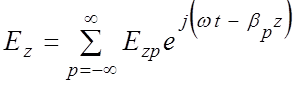  ,                    (3.5)

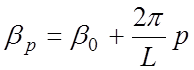где                             ;    .                               (3.6)

Выражение (3.5) представляет собой сумму бесконечного числа волн с разными амплитудами E_zр, фазовыми постоянными β_р и одинаковыми частотами ω. Эти волны называются пространственными гармониками     (в отличие от временных гармоник). Каждая гармоника имеет свой     номер р. Поскольку фазовые постоянные β_р зависят от номера, пространственные гармоники имеют разные фазовые скорости υ_фр и длины замедленных волн λ_3р.

По определению υ_фр 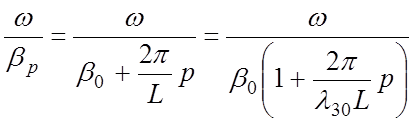 =  и .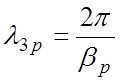

Так как    υ_ф0 = ; 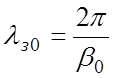, то

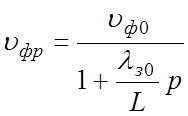.                                          (3.7)

Групповые скорости всех гармоник одинаковы, так как

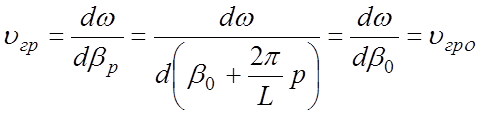.                     (3.8)

Выразим групповую скорость через фазовую. Так как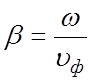, то

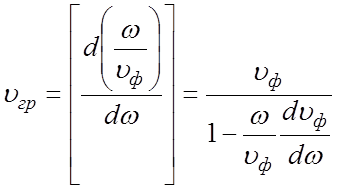                       .                               (3.9)

Из (3.9) следует, что при нормальной дисперсии, когда 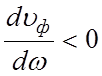, групповая скорость тем меньше, чем больше дисперсия. В отсутствие дисперсии групповая и фазовая скорости совпадают. Направление групповой скорости  волны задается возбуждающим устройством. Гармоника, имеющая наибольшую амплитуду и фазовую скорость, называется основной. Обычно это нулевая гармоника. С ростом номера амплитуды гармоник уменьшаются.

Гармоники, отличающиеся знаком р, имеют противоположные направления фазовой скорости. Гармоники с номером р  0 называются положительными или прямыми, если р < 0, то гармоники называются отрицательными или обратными. Положительные гармоники имеют одинаковые направления фазовой и групповой скорости, для отрицательных гармоник направления фазовой и групповой скоростей противоположны.

          Гармоники существуют только совместно и определяют общую структуру поля в ЗС, зависящую от её геометрии и частоты. Соотношение между амплитудами гармоник не зависит от мощности возбуждения, а также определяется только геометрией ЗС. Как было сказано в начале главы, в некоторых ЗС с малым по сравнению с длиной волны периодом амплитуда нулевой гармоники существенно преобладает над высшими и ими можно пренебречь.

          3.2. Дисперсионные характеристики замедляющих систем

          В первую очередь, свойства замедляющих систем определяют дисперсионные характеристики.

          Под дисперсионной характеристикой понимают зависимость фазовой скорости от частоты или длины волны. Однако на практике эти характеристики удобнее рассматривать в виде зависимости коэффициента замедления от длины волны λ или от относительной   длины волны .

          В некоторых случаях дисперсионные характеристики строят в других координатах – к, β, где к и β – волновые числа в свободном пространстве и замедляющей системе. Эти характеристики также позволяют определить фазовую и групповую скорости на любой частоте в полосе пропускания.

          Рассмотрим качественный вид дисперсионных характеристик            к = к (β). Как было показано выше, фазовые постоянные гармоник β_р зависят от их номера р. Поэтому фазовый сдвиг гармоники на период системы φ_Lp также зависит от р  или

.                                      (3.10)