В области II фаза поля в пределах одной ячейки предполагается неизменной. То есть в этой области имеются только стоячие волны. Распределение составляющих поля в области II внутри каждой ячейки можно представить в виде ряда, однако на практике можно ограничиться лишь первым его членом
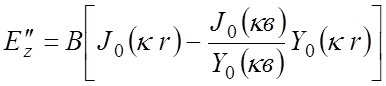 ,
,
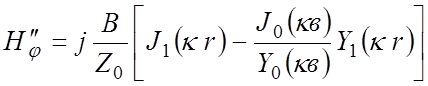 , где
, где
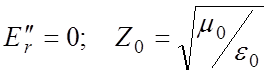 , В – некоторая постоянная, определяемая также
из условия непрерывности Ez. Для сшивания полей на границе областей необходимо
знать истинное распределение Ez (z) по линии
, В – некоторая постоянная, определяемая также
из условия непрерывности Ez. Для сшивания полей на границе областей необходимо
знать истинное распределение Ez (z) по линии ![]() .
.
Достаточно точно это распределение аппроксимируется квазистатическим приближением вследствие малости размера d по сравнению с длиной волны
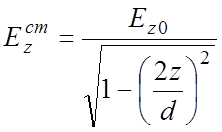 ,
,
где
Ez0 –
напряженность поля в центре зазора, координата 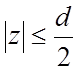 отсчитывается
от середины зазора между диафрагмами. За пределами этого интервала в пределах
периода
отсчитывается
от середины зазора между диафрагмами. За пределами этого интервала в пределах
периода ![]() . Усреднение
. Усреднение ![]() и
и
![]() по периоду системы позволяет
определить амплитуды гармоник
по периоду системы позволяет
определить амплитуды гармоник
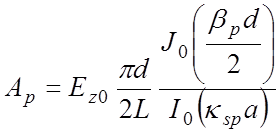 .
.
Усреднение
![]() и
и ![]() позволяет
выразить постоянную В также через
позволяет
выразить постоянную В также через ![]()
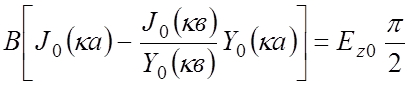 .
.
Дисперсионное
уравнение получается приравниванием усредненного при ![]() магнитного
поля
магнитного
поля ![]() магнитному полю
магнитному полю ![]() . Входящая в оба эти соотношения
величина Ez0 при этом
сокращается, а уравнение принимает следующий вид:
. Входящая в оба эти соотношения
величина Ez0 при этом
сокращается, а уравнение принимает следующий вид:
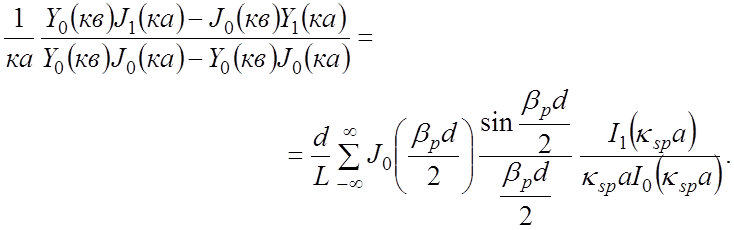 (4.16)
(4.16)
Следует отметить, что решение трансцендентного уравнения (4.16) требует большой вычислительной работы.
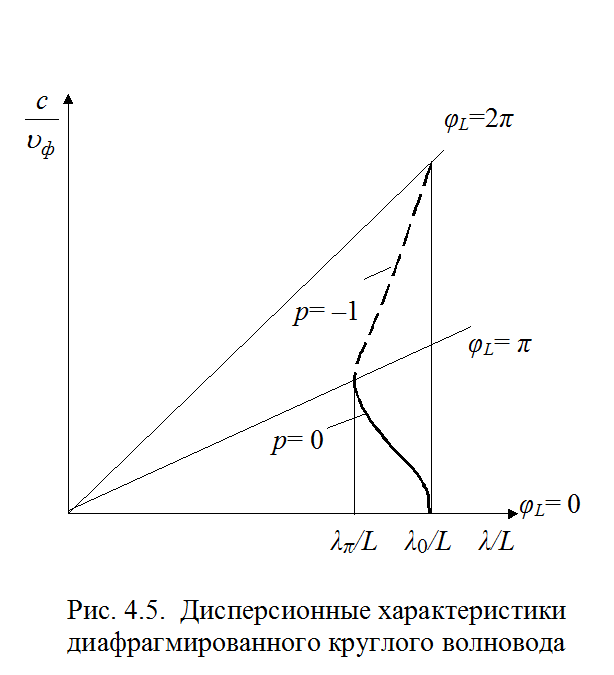 |
Следует отметить узкую полосу частот, в которой коэффициент замедления нулевой гармоники n > 1, а также малую его величину.
![]()
4.4. Замедляющая система типа цепочки индуктивно связанных резонаторов
Замедляющие системы типа цепочек связанных резонаторов (ЦСР) обычно используются в ЛБВ большой мощности. Среди различных ЗС типа ЦСР, отличающихся формой резонаторов, способом связи между ними, наиболее распространены системы с ячейками в виде тороидальных резонаторов с одной щелью связи, расположенной в периферийной, индуктивной части резонатора, и углом поворота щелей в соседних ячейках, равным 180º. Сложность расчета таких систем путем строгого решения электродинамической задачи обусловлена ее трехмерностью из-за наличия щелей связи. Имеются программы численного расчета таких систем, однако они не обеспечивают достаточной точности и часто требуют в процессе их использования дополнительных экспериментальных данных.
Рассмотрим методику расчета таких систем, основанную на модели эквивалентных схем и на определении параметров элементов эквивалентной схемы по результатам численного решения электродинамической задачи.
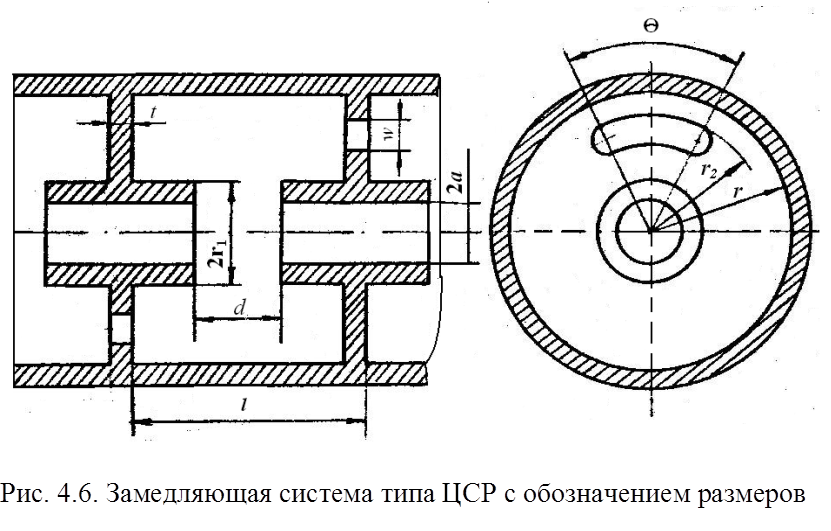 |
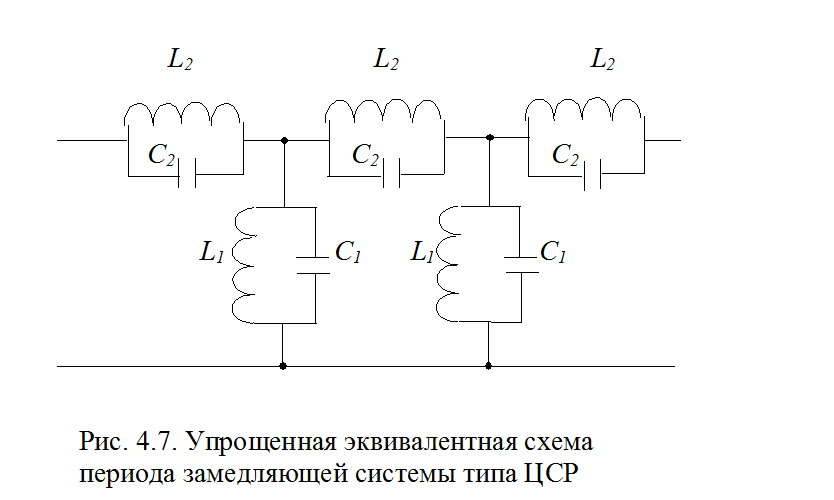 |
В схеме не учтен поворот щелей связи в соседних резонаторах. Индекс «1» на обозначениях элементов относится к резонатору, а индекс «2» – к щели.
Для
построения дисперсионных характеристик используем уравнение (3.11), в котором ![]() определяется из уравнения (4.3).
Преобразуем (4.3) применительно к схеме рис. 4.7, определив Z иY:
определяется из уравнения (4.3).
Преобразуем (4.3) применительно к схеме рис. 4.7, определив Z иY:
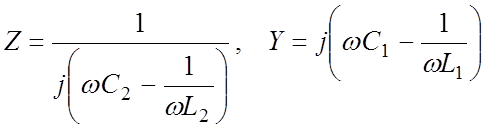 , (4.17)
, (4.17)
и подставив их в (3.11)
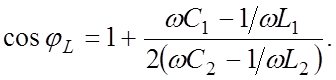 (4.18)
(4.18)
Определим вначале граничные частоты (длины волн).
Граничная
частота ω0 соответствует ![]() ,
и из (4.18) следует
,
и из (4.18) следует
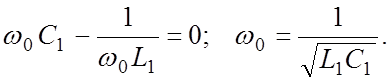 |
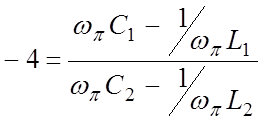 или после преобразований
или после преобразований
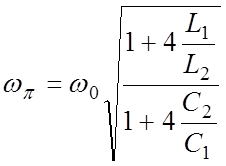 . (4.19)
. (4.19)
Из (4.19) следует, что ![]() , если
, если ![]() , то есть резонансная длина волны
резонатора больше резонансной длины волны щели, что имеет место в большинстве
реальных конструкций. В результате получаются дисперсионные характеристики,
показанные на рис. 4.8. Поскольку
, то есть резонансная длина волны
резонатора больше резонансной длины волны щели, что имеет место в большинстве
реальных конструкций. В результате получаются дисперсионные характеристики,
показанные на рис. 4.8. Поскольку ![]() , то основная
гармоника имеет нормальную и положительную дисперсию. На этом же рисунке
показаны также дисперсионные характеристики во второй полосе пропускания,
обусловленные резонансом щели связи.
, то основная
гармоника имеет нормальную и положительную дисперсию. На этом же рисунке
показаны также дисперсионные характеристики во второй полосе пропускания,
обусловленные резонансом щели связи.
Для расширения основной полосы пропускания резонаторной ЗС щели связи
в смежных резонаторах сдвигают на 180˚. При этом эквивалентная схема
существенно усложняется. Такая уточненная эквивалентная схема периода системы
показана на рис. 4.9. Между контурами, эквивалентными резонатору и щелям связи,
дополнительно включены индуктивности, связанные с токами, которые
перехватываются щелями. Учтено также противонаправленное расположение щелей в
соседних резонаторах. Параметр 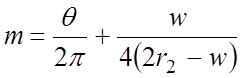 ; θ –
угловой раскрыв регулярной части щели.
; θ –
угловой раскрыв регулярной части щели.
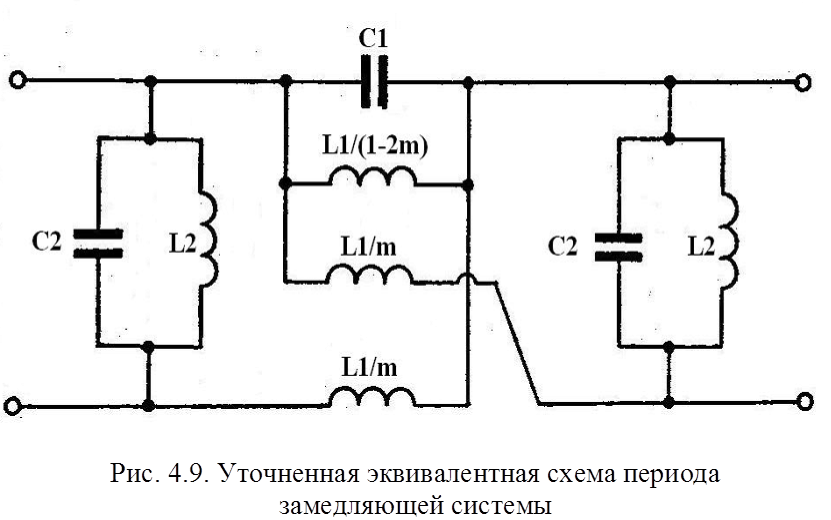
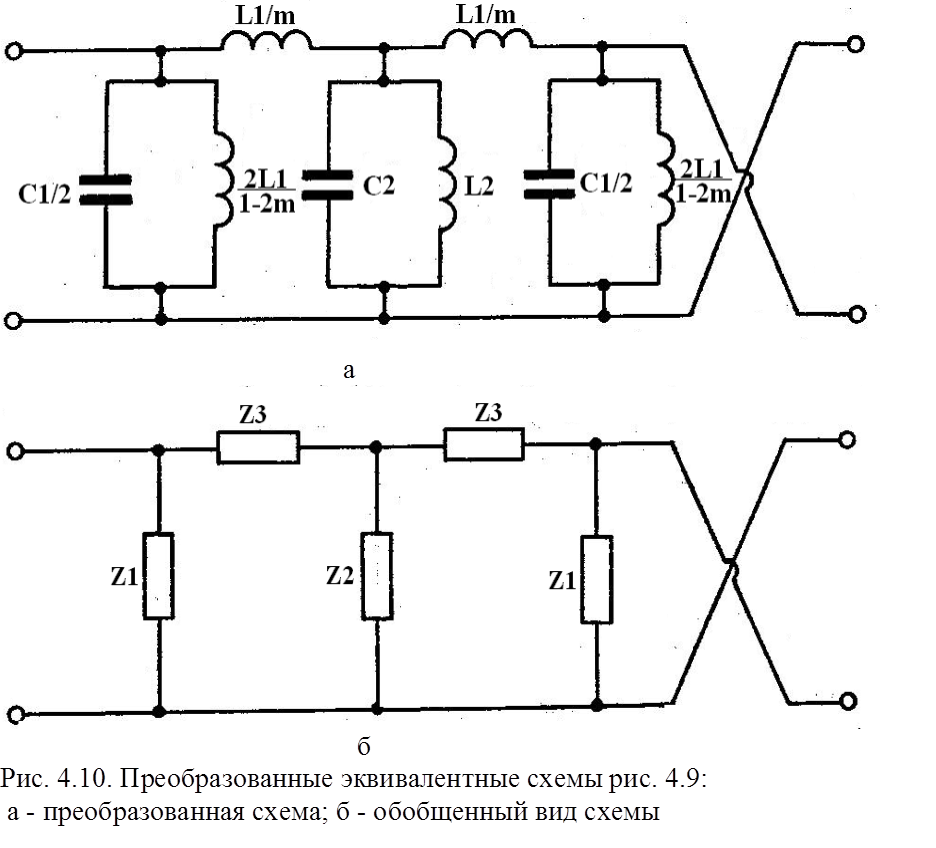
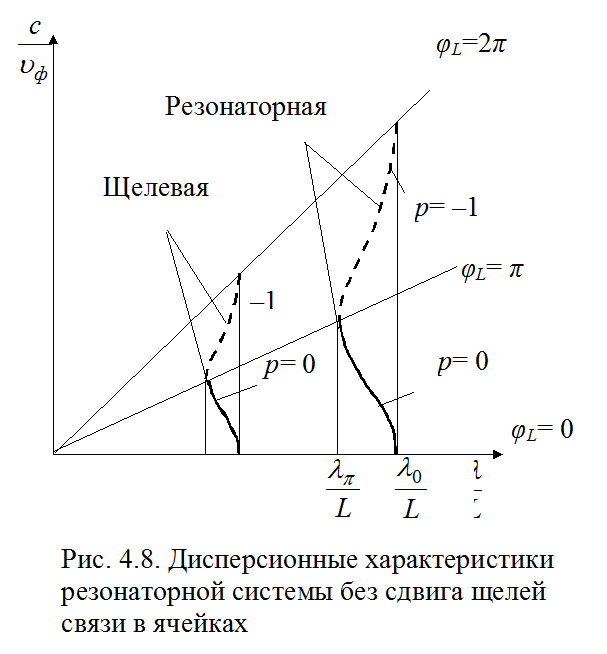 Схема может быть преобразована к виду, показанному на
рис. 4.10,а, и представлена в обобщенном виде (рис. 4.10,б), где используются
следующие обозначения:
Схема может быть преобразована к виду, показанному на
рис. 4.10,а, и представлена в обобщенном виде (рис. 4.10,б), где используются
следующие обозначения:
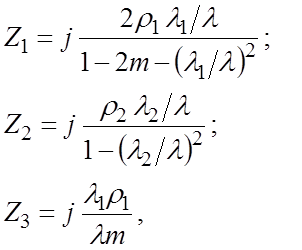 где
где 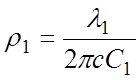 - характеристическое сопротивление
резонатора,
- характеристическое сопротивление
резонатора, 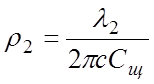 – характеристическое
сопротивление щели, λ1 , λ2 – резонансные
длины волн резонатора и щели на низших видах колебаний, λ – текущая
длина волны, с = 3·1010 см/с – скорость света в вакууме.
– характеристическое
сопротивление щели, λ1 , λ2 – резонансные
длины волн резонатора и щели на низших видах колебаний, λ – текущая
длина волны, с = 3·1010 см/с – скорость света в вакууме.
 |
Фазовый сдвиг на период системы определяется через диагональные элементы матрицы передачи эквивалентного четырехполюсника:
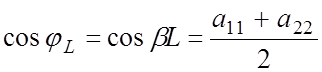 ,
,
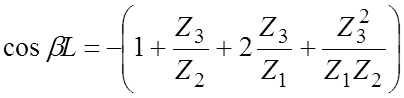 .
(4.20)
.
(4.20)
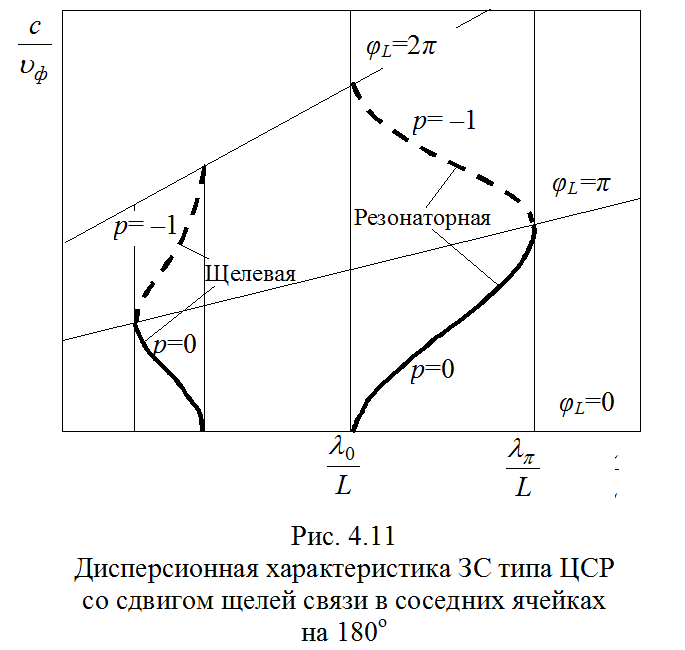 На рис. 4.11 показаны дисперсионные характеристики ЗС
типа ЦСР с противонапра-вленными щелями связи. Сле-дует отметить, что
основная гармоника имеет аномальную и отрицательную дисперсию, а
га-рмоника р = –1 – положительную. В данном случае для нумерации гармоник
иногда используют индекс р΄=р+1. При такой нумерации основной
является гармоника р΄ = 0, име-ющая положительную дисперсию. В
коротковолновой части показаны также щелевые дисперсионные характеристики. С
целью расширения полосы пропускания ЗС увеличивают угол раскрыва щели связи;
при этом основная и щелевая полосы пропускания могут перекрываться.
На рис. 4.11 показаны дисперсионные характеристики ЗС
типа ЦСР с противонапра-вленными щелями связи. Сле-дует отметить, что
основная гармоника имеет аномальную и отрицательную дисперсию, а
га-рмоника р = –1 – положительную. В данном случае для нумерации гармоник
иногда используют индекс р΄=р+1. При такой нумерации основной
является гармоника р΄ = 0, име-ющая положительную дисперсию. В
коротковолновой части показаны также щелевые дисперсионные характеристики. С
целью расширения полосы пропускания ЗС увеличивают угол раскрыва щели связи;
при этом основная и щелевая полосы пропускания могут перекрываться.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.