Замедляющие системы (основные свойства, характеристики, теоретические и экспериментальные методы исследования замедляющих систем): Учебное пособие, страница 2

          Как известно, тригонометрические функции мнимого аргумента можно заменить соответствующими гиперболическими функциями от вещественного аргумента, следовательно,

E_z = A chκ_sy + B shκ_sy,                                       (1.9)

где κ_s = 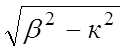 - поперечное волновое число можно также представить в виде

κ_s = 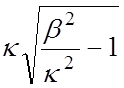;                                         (1.10)

κ_s = .                                          (1.10а)

Таким образом, поле в поперечном сечении замедляющей системы с плоской симметрией описывается монотонными гиперболическими функциями в области распространения замедленной волны (y < ).

Следовательно, составляющая Е_z не может обращаться в ноль на всех граничных поверхностях, поскольку гиперболические функции имеют не более одной нулевой точки.

          В рассматриваемом случае из граничного условия Е_z = 0 при у = 0 следует, что А = 0 и

Е_z = Вshκ_sy.                                                (1.11)

          Распределение Е_z по оси у  в соответствии с (1.11) показано на рис. 1.1,б. На поверхности гребенки (у = ) Е_z  принимает максимальное значение и быстро убывает при удалении от нее. С ростом частоты постоянная κ_s увеличивается, и скорость убывания Е_z  при удалении от гребенки также растет. Следовательно, чем выше частота, тем в большей степени поле сосредотачивается вблизи гребенки.

Для случая двусторонней гребенки, имеющей плоскость симметрии,

                                          Е_z = Асhκ_sy.

На поверхности гребенки имеются также не равные нулю другие составляющие электромагнитного поля. Определим магнитное поле, используя известное из теории волноводов соотношение, связывающее его поперечные составляющие с продольной составляющей электрического поля.

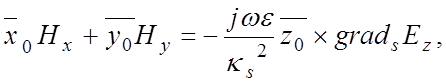                        (1.12)

где единичные орты в направлении осей ; H_x, H_y – поперечные составляющие вектора магнитного поля, ε- диэлектрическая проницаемость среды в линии, grad_s - градиент в поперечном сечении.

Для случая 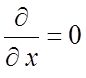,   H_y = 0 и из (1.11) и (1.12) получаем

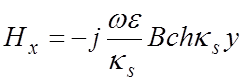.                                      (1.13)

Отношение составляющих Е_z и H_x позволяет определить поверхностное сопротивление (импеданс)  гребенки Z_xпо (1.11) и (1.13)

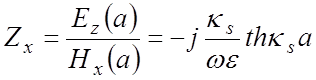_.                                             (1.14)

          В соответствии с (1.14) поверхностное сопротивление гребенки имеет реактивный характер. Это свойство, присущее любой замедляющей системе, свидетельствует о том, что для получения замедленной волны, по крайней мере, одна из граничных поверхностей линии должна иметь реактивное поверхностное сопротивление. Такое сопротивление реализуется на поверхности с периодически изменяющимися граничными условиями.

1.2. Структура поля в поперечном сечении замедляющих систем,

 обладающих осевой симметрией

В качестве примера рассмотрим систему типа круглый волновод с тонкими диафрагмами (рис.1.2). Период L считаем малым по сравнению с длиной замедленной волны. Считаем также, что поле соответствует низшему типу волны Е, т.е. обладает осевой симметрией  (;  φ – угловая координата).

Тогда волновое уравнение для продольной составляющей электрического поля Е_z  в цилиндрической системе координат принимает вид

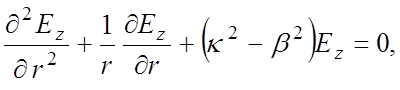                               (1.15)

где r – радиальная координата.

          Уравнение (1.15) – уравнение Бесселя – имеет решение в виде комбинации функций Бесселя первого и второго рода нулевого порядка J₀ и Y₀

.

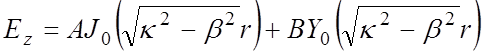При условии замедления выполняется неравенство (1.4) и можно воспользоваться обозначением (1.8). Тогда

.

Заменим функции Бесселя мнимого аргумента модифицированными функциями Бесселя вещественного аргумента

.                                (1.16)

Модифицированные функции Бесселя первого и второго рода нулевого порядка I₀ и K₀ подобно гиперболическим функциям имеют монотонный характер и только один ноль. Некоторые из этих функций показаны на  рис. 1.3.

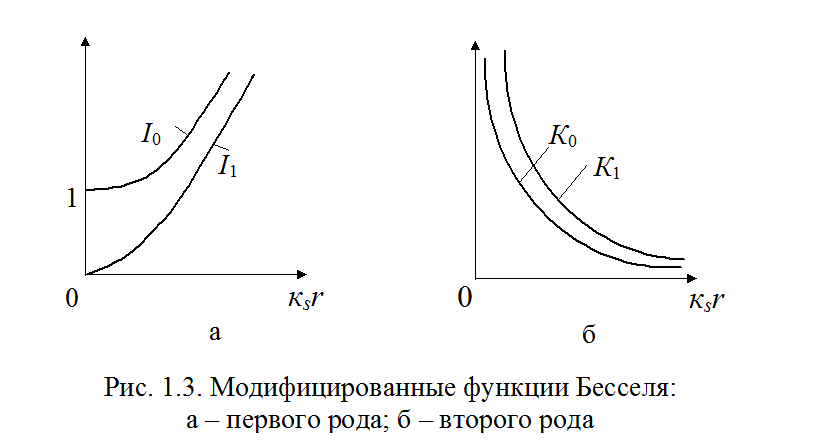          Поскольку функция К₀ при нулевом аргументе обращается в бесконечность, то из физически очевидного условия конечности величины поля следует  в (1.16) положить В = 0.

          Тогда в круглом диафрагмированном волноводе в области      распределение Ε_z  по радиальной координате описывается выражением

                                         (1.17)

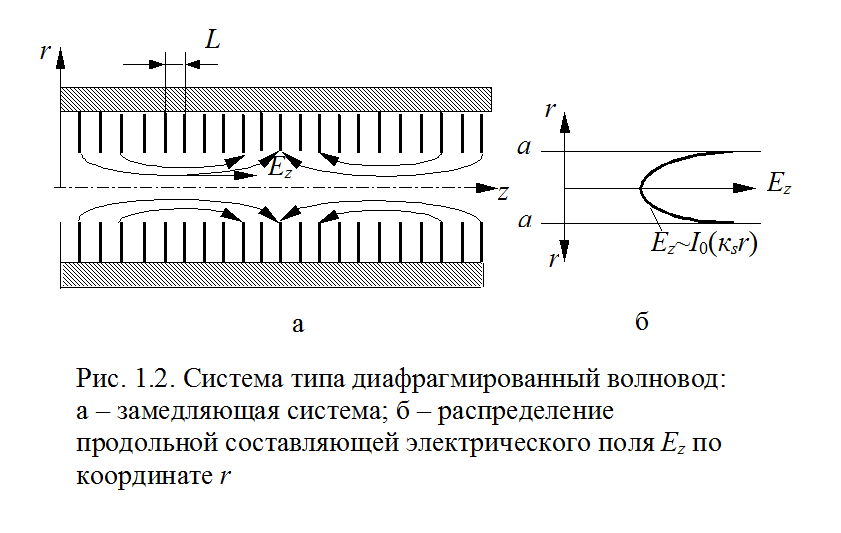
Соответствующая (1.17) эпюра показана на рис. 1.2,б.

     Как и в случае гребенки, продольная составляющая электрического поля принимает максимальное значение на цилиндрической поверхности , совпадающей с поверхностью, ограниченной диафрагмами, и быстро убывает при удалении от этой поверхности к оси системы.

     Можно также показать, что на этой поверхности сопротивление не равно нулю, а имеет реактивный характер.

2.  Основные типы периодических замедляющих систем

Как было показано в предыдущей главе, замедление волн в линии возможно в том случае, если, по крайней мере, одна из её поверхностей имеет периодические граничные условия вдоль направления распространения волны. На практике эти условия реализуются с помощью проводников, имеющих различную конфигурацию. В зависимости от назначения созданы замедляющие системы, имеющие самые разнообразные конструкции, не поддающиеся строгой классификации.

Тем не менее, можно выделить следующие основные типы замедляющих систем: спиральные, стержневые, диафрагмированные линии передач – гребенчатые структуры, резонаторные и ряд других. Каждый из типов имеет различные модификации, отличающиеся видом симметрии, геометрией, размерами неоднородностей и другими признаками.

2.1. Спиральные замедляющие системы

Наиболее простой замедляющей системой, получившей широкое распространение при создании широкополосных ламп бегущей волны малой и средней мощности, является однозаходная спираль (рис. 2.1,а).

В основе замедления волны  в спиральной линии лежит простая идея. Увеличение пути электромагнитной волны вдоль спирального проводника приводит к уменьшению её скорости в осевом направлении.