Начертим график этих данных и выведем плановую цифру 50 на начало января, т.е. в точке (0; 50) Проведем прямую y = 50 и у нас сразу будет видно отклонение от плана (рис. 15.2).
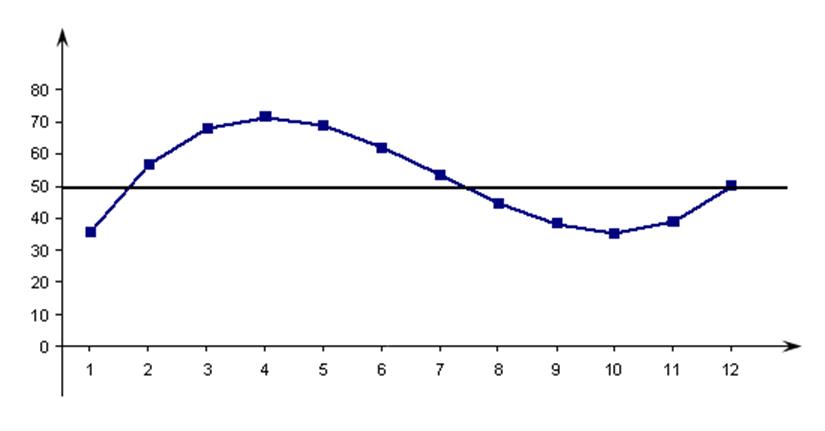
Рис 15.2
О чем говорит полученная информация? Ответим согласно условию задачи. Процент выполнения плана (пятая строка) вычислялся из пропорции
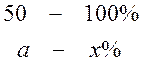
Откуда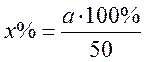 
, где а – число во второй
строке таблицы. Так, в январе процент выполнения плана составил 35,3 100% : 50
= 70,6%, в феврале 56·100% : 50 = 113,4% и так далее. Последняя цифра 103,6%
показывает среднегодовое выполнение плана. Ее можно рассчитать как среднее
значение помесячных данных, или по той же пропорции:
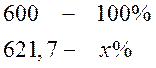
Результат получится одинаковым.
Ответ на второй вопрос тоже очевиден: наиболее успешным был период с февраля по июнь, «провальным» – август-ноябрь.
А теперь проанализируем данные третьей и четвертой строки таблицы. Первая разность характеризует цепной прирост и говорит, на сколько изменился показатель за месяц. Положительные приросты говорят о положительной динамике процесса, т.е. о возрастании объема выпуска продукции. Этому условию отвечают данные с первого по пятый месяц. С пятого по десятый месяцы наблюдался стойкий спад, их приросты всюду отрицательны, и только в декабре предприятию удалось выйти на плановый показатель. Наибольшую скорость возрастания имел февраль 21,4 млн. руб./мес., наименьшую – апрель, когда начался спад.
О чем говорит содержимое четвертой строки? Об ускорении процесса. Несмотря на фиксируемый подъем в начале года, уже к марту наблюдалось замедление скорости прироста – вторые разности становятся отрицательными, и такая картина продержалась до сентября. Именно тогда ускорение сменило знак с отрицательного на положительный, и предприятие стало медленно, но верно выползать из «нижней» зоны, хотя на первый взгляд данных для оптимизма не было. Эта точка называется точкой перегиба, начиная с которой, как говорят политики, «можно увидеть свет в конце туннеля» и делать осторожные прогнозы относительно последующего хода событий.
Такие чисто экономические показатели как темп роста и темп прироста показывают во сколько раз данная цифра отличается от предыдущей или плановой.
Так «работают» первая и вторые производные в экономических задачах.
ПЛАН
1. Введение.
2. Функция двух переменных. Способы задания. Область определения.
3. Приращения функции: частное и полное.
4. Непрерывность.
5. Частные производные первого порядка
6. Дифференциал
7. Заключение.
Очень немногие процессы зависят от одной переменной. Жизнь многогранна и зависит от многих факторов. Например, площадь прямоугольника S является функцией его ширины x и длины y, объем параллелограмма V – ширины x, длины y и высоты z и т.д. В первом случае мы имеем дело с функцией двух переменных, во втором – трех переменных. Нетрудно привести примеры, когда в определяющее число факторов будут входить четыре и большее число переменных. Функцию одной переменной мы изучили достаточно полно, перейдем теперь к функции двух переменных.
Определение 16.1. Если каждой паре (х, у) значений двух независимых друг от друга переменных величин х и у из некоторой области их изменения D соответствует определенное значение величины z, то говорят, что z является функцией от x и y в области D.
Символически функция двух переменных обозначается так:
.
Как и функция одной переменной она может быть задана аналитически, таблично и графически. Переход от одного способа задания к другому осуществляется по тем же правилам, что и для функции одной переменной.
Пусть функция
задана формулой 
. Составим для нее таблицу
значений, в первой строке которой будут находиться значения х, а в
первом столбце – значения у. Выберем произвольные значения для х
и у, а z получается согласно заданному
правилу.
|
x y |
0,1 |
0,2 |
0,3 |
0,4 |
|
1 |
0,2 |
0,4 |
0,6 |
0,8 |
|
2 |
1,2 |
1,4 |
1,6 |
1,8 |
|
3 |
2,2 |
2,4 |
2,6 |
2,8 |
|
4 |
3,2 |
3,4 |
3,6 |
3,8 |
|
5 |
4,2 |
4,4 |
4,6 |
4,8 |
Для того чтобы построить график этой функции нужно из каждой точки М(х,у) плоскости ХОY поднять перпендикуляр z и потом объединить полученные точки аппликат. Следует учесть, что графическое изображение функции двух переменных в трехмерном декартовом базисе в общем случае представляет некоторую поверхность. В лекции 8 мы показывали, что построение линии «по точкам» страдает приближенностью и даже ошибочностью, потому что не может учесть такие важные точки, как разрывы, экстремумы и т.д. Поэтому если надо построить график поверхности, решают вопрос в общем виде, определив ее тип, а потом переходят к построению.
Если на плоскости самая простая и самая изученная линия – это прямая, то наиболее простая поверхность в пространстве – это плоскость, уравнение которой в общем виде записывается так:
. (16.1)
Разделив обе части равенства на D, получим равносильное уравнение
,
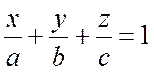(16.2)
где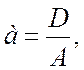 
,
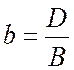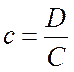. Его называют уравнением
плоскости «в отрезках».
По полученному уравнению (16.2) легко изобразить
плоскость в декартовой системе координат. Найдем точки ее пересечения с осями
координат: с осью ОХ : 
, 
,
с осью ОY: 
, 
,
и с осью ОZ: , 
. Соединим полученные точки,
продолжая их во все стороны, и получим изображение плоскости.
Для нашего
случая 
, 
, 
, 
.
Построим эту плоскость по точкам
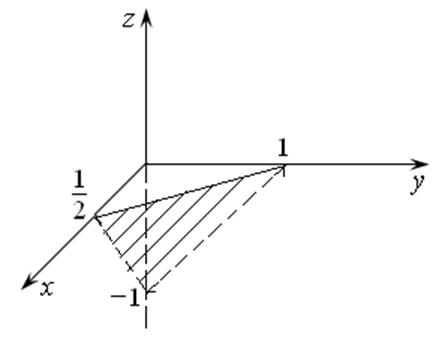
Рис. 16.1
В разделе «Аналитическая геометрия» мы также изучили кривые второго порядка – окружность, эллипс, гиперболу и параболу. В трехмерном пространстве они перешли в сферу, эллипсоид, гиперболоид (однополостный и двуполостный) и параболоид. В сечении этих тел плоскостями, параллельными координатным плоскостям, получаются все те же окружность, эллипс и т.д. Но на этом дело не закончилось. Кривые, вырвавшись в трехмерное пространство, создали эллиптический гиперболоид, гиперболический параболоид, конические и цилиндрические поверхности. Перечень поверхностей второго порядка и их графики приведены в приложении 1. Вглядитесь в их уравнения и постарайтесь понять логику их названий.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.