Теоремы о дифференцируемых функциях. Исследование поведения функции. Приложения производных к экономическим задачам. Функции многих переменных, страница 5

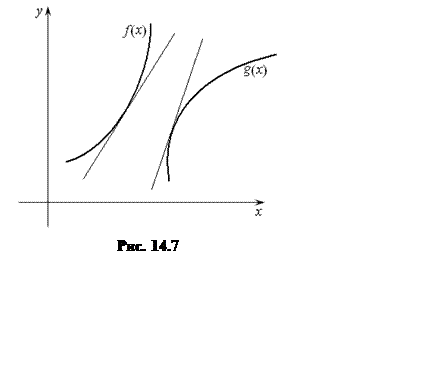
Посмотрите на графики функций  и  на рис. 14.7. Они обе возрастают, но характер их возрастания различный:  сначала медлит, а потом резко взлетает вверх,  – наоборот: сначала взлетает, а потом ее скорость убывает. Различаются графики и по форме. Первый является вогнутым, второй – выпуклым, и это наблюдение связано с интуитивным наблюдением подобных кривых.

Дадим более строгое математическое определение вогнутости и выпуклости формы графика, а затем найдем признаки, по которым будем судить о наличии этих характеристик.

Определение 14.4. График дифференцируемой функции  называется выпуклым на интервале , если он расположен ниже любой своей касательной на этом интервале.

Определение 14.5. График дифференцируемой функции  называется вогнутым на интервале , если он расположен выше любой своей касательной на этом интервале.

Определение 14.6. Точка графика непрерывной функции, отделяющая ее выпуклую часть от вогнутой, называется точкой перегиба(рис. 14.8).

Точки  и  – точки перегиба.

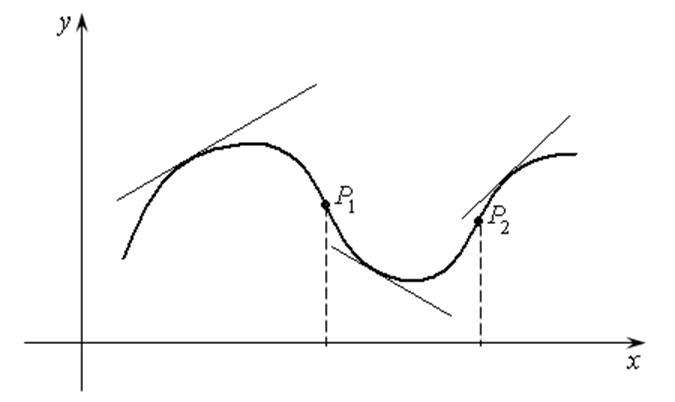
Рис. 14.8

Отметим, что условия выпуклости и вогнутости функции на некотором интервале, а также условия существования точек перегиба, формулируются точно также как и условия монотонности функции и существование точек экстремума, но для функции .

Теорема 14.7. (необходимое условие выпуклости функции). Пусть  непрерывна вместе со своими производными  и  до второго порядка включительно на . Для того, чтобы ее график был выпуклым на интервале  необходимо, чтобы .

Доказательство.

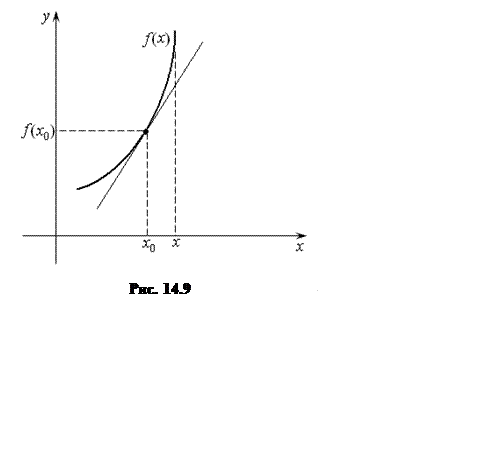
Для доказательства этого утверждения возьмем любую точку  и составим уравнение касательной в этой точке, как уравнение прямой, проходящей через точку  с угловым коэффициентом равным  (рис. 14.9):

.

Возьмем вторую точку  (для определенности, хотя может быть и меньше) и найдем разность ординат графика  и касательной . Получаем

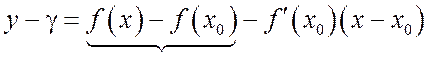                           (14.1)

Применим к выделенной разности  теорему Лагранжа:

,

где точка . Подставим получившееся выражение в (14.1):

.

К последней разности еще раз применим теорему Лагранжа и получим:

,                (14.2)

где . Учтем, что  и , тогда .

По условию теоремы дано:  – выпуклый на .

Требуется доказать: .

Так как график функции выпуклый, то любая его касательная лежит выше него, поэтому в равенстве (14.2) левая часть  отрицательна. Следовательно, и правая часть должна быть отрицательной, а это возможно лишь при условии , а в пределе при  получим . Что и требовалось доказать.

Теорема 14.8 (достаточное условие выпуклости функции). Пусть  непрерывна вместе со своими производными  и  до второго порядка включительно на . Если , то график функции  будет выпуклым на интервале .

Доказательство.

Дано:

Доказать:  – выпукла.

Теперь работаем с известной правой частью равенства (14.2). Она отрицательна, т. к.  и , поэтому и левая часть должна быть отрицательна, т. е  или , что и говорит о выпуклости графика.

Запишем формулировки рассмотренных теорем символически следующим образом:

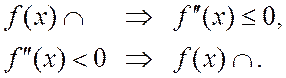
Необходимый и достаточный условия вогнутости графика формулируется аналогично.

Теорема 14.9 (необходимые условие вогнутости функции). Пусть  непрерывна вместе со своими производными  и  до второго порядка включительно на . Для того, чтобы ее график был вогнутым на интервале  необходимо, чтобы .

Теорема 14.10 (достаточное условие вогнутости функции). Пусть  непрерывна вместе со своими производными  и  до второго порядка включительно на . Если , то график функции  будет вогнутым на интервале .

Символически эти теоремы можно записать так:

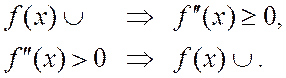
Доказательство этих теорем проведите самостоятельно.

Нахождение точек перегиба основано на следующей теореме.

Теорема 14.11 (необходимое и достаточные условия существования точек перегиба). Пусть функция  непрерывна вместе со своими производными  и  на . Для того, чтобы точка  была точкой перегиба, необходимо, чтобы  (или не существовала) и достаточно, чтобы  меняла свой знак при переходе через .

Этот признак сразу регламентирует порядок действий:

1. Находим .

2. Решаем уравнение  и находим точки, подозрительные на точки перегиба. Туда же входят и точки, где  не существует.

3. Смотрим знак  слева и справа от полученных точек и на всех интервалах непрерывности функции.

4. Делаем выводы об интервалах выпуклости, вогнутости и точек перегиба. Находим ординаты точек перегиба.

Как мы видим, порядок действий аналогичен порядку действий для определения интервалов возрастания, убывания функции и точек экстремумов.

Пример 14.2. Определить интервалы выпуклости – вогнутости и точки перегиба функции .

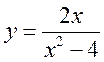Решение: Область допустимых значений этой функции

.

Первая производная этой функции была найдена на прошлой лекции:

.

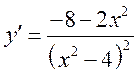Поэтому продолжаем далее.

1. .

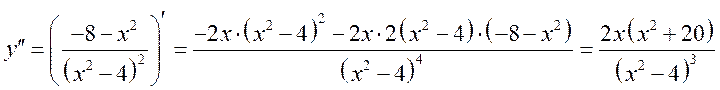2. , если , . Единственная точка, подозрительная на перегиб, это точка .

3. Рисуем таблицу знаков  с учетом интервалов непрерывности и сразу делаем выводы.

x	, знак	вывод
	– < 0	выпуклый Ç
	+ > 0	вогнутый È
0	0	точка перегиба
	–	выпуклый Ç
	+	вогнутый Ç

Чертим график.

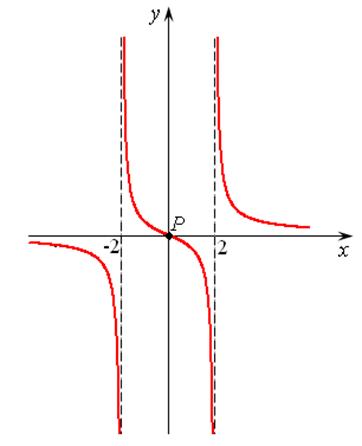
Рис. 14.10

Пример 14.3. Определить интервалы выпуклости – вогнутости и точки перегиба функции .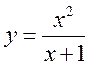

Решение: Область допустимых значений этой функции

Первая производная этой функции также была найдена на прошлой лекции:

.

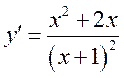Продолжаем далее.

1.

.

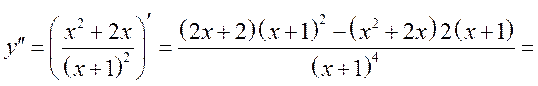
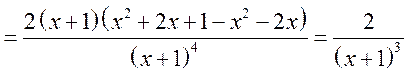2. , точек перегиба нет, т.к. числитель этой дроби отличен от нуля. Поэтому определим знак  на интервалах непрерывности.

     кривая выпукла,

,         кривая вогнута.

График этой функции был приведен на прошлой лекции (рис. 14.6).

14.7. Асимптоты функции

С понятием асимптоты, т. е. прямой, к которой стремятся точки графика функции  при неограниченном удалении от начала координат, мы знакомились на примере гиперболы (см. тему «Аналитическая геометрия»). Поскольку любая прямая в декартовой системе координат может быть либо параллельна осям координат, либо наклонена под произвольным углом  к оси , то и асимптоты могут быть горизонтальными, вертикальными и наклонными (рис. 14.11).