1. На интервале
![]() возьмем значение p = 100. В этом случае эластичность равна
возьмем значение p = 100. В этом случае эластичность равна 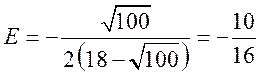 , т.е.
, т.е. ![]() . Спрос
при этих значениях цен является неэластичным: цена на товар растет быстрее, чем
уменьшается на нее спрос.
. Спрос
при этих значениях цен является неэластичным: цена на товар растет быстрее, чем
уменьшается на нее спрос.
2. На
интервале ![]() возьмем значение p = 225. В этом случае эластичность равна
возьмем значение p = 225. В этом случае эластичность равна 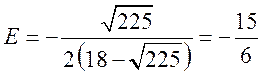 , т.е.
, т.е. ![]() .
Спрос при этих значениях цен является эластичным: спрос на товар падает
быстрее, чем растут на нее цены.
.
Спрос при этих значениях цен является эластичным: спрос на товар падает
быстрее, чем растут на нее цены.
Какие можно дать рекомендации? Если цена единицы продукции составит 100 ден. ед., то спрос будет неэластичным и можно повысить цену продукции, выручка при этом будет расти. При стоимости 225 ден. ед. спрос является неэластичным. В данном случае целесообразно рассмотреть предложения о снижении цены, выручка будет расти в результате увеличения спроса на продукцию.
В экономической практике все количественные изменения какого-либо признака (прибыли, числа продаж, затрат на организацию производства) компонуются и представляются таблицей. Для более наглядного обозрения процесса привлекают графики и диаграммы. Рассмотрим возможности дифференциального исчисления для описания функции, заданной таблично.
Проведем математическое исследование экономической задачи по тому же плану, который мы обозначили в предыдущей главе.
1 Область допустимых значений аргумента и область значений функции. Точки разрыва.
2. Точки пересечения с осями координат.
3. Интервалы возрастания – убывания, точки экстремумов.
4. Интервалы выпуклости – вогнутости, точки перегиба.
Такие характеристики, как симметрия и асимптоты мы опустим, ввиду ограниченности и неотрицательности временного интервала, на котором рассматривается любая экономическая задача. Коротко осветим все особенности указанных пунктов, для функции, заданной таблично.
Итак, пусть функция задана таблицей.
|
Янв. |
Февр. |
Март |
Апр. |
Май |
Июнь |
Июль |
Авг. |
Сент. |
Окт. |
Нояб. |
Дек. |
|
9,1 |
11,2 |
– |
6,4 |
3,1 |
0 |
2,6 |
3,1 |
2,0 |
–1,2 |
–3,1 |
2 |
1. Областью ее определения является перечень всех значений аргумента Х [1, 12] месяцев, а могут быть кварталы, годы и т.д. Область значений функции – от самого малого до самого большого Y Î [–3,1; 11,2] Это, как правило, деньги, например – прибыль. Точками разрыва являются точки, где отсутствует информация. Об этом говорит прочерк (март). Заменять прочерк нулем нельзя: март может быть нерабочим месяцем, где прибыль равна нулю, либо настолько выдающимся, что о ней лучше умолчать (рис. 15.1).
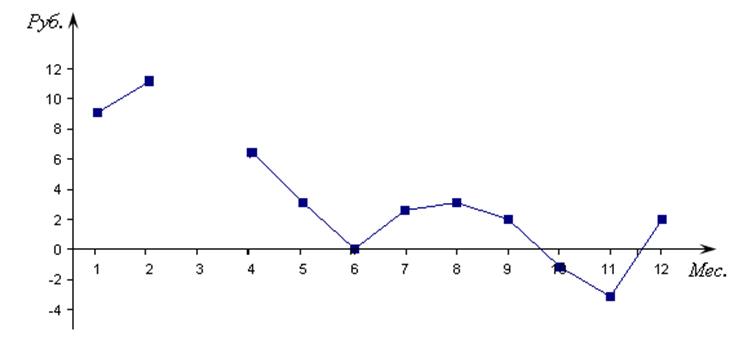
Рис. 15.1
2. Точки пересечения с осью абсцисс найти легко – это точки, где у = 0 или меняет свой знак. В нашем случае это июнь, и промежутки сентябрь – октябрь, ноябрь – декабрь. Эти точки называются корнями функции. Точки пересечения с осью ОY специального названия не имеют. В экономических таблицах – это остаток на 1 января, плановая составляющая на каждый месяц, либо другая информативная цифра, с которой в дальнейшем идет сравнение.
3. Интервалы возрастания-убывания и точки экстремумов.
Напомним, что функция называется возрастающей, если большему значению Х
соответствует большее значение Y и убывающей в противном
случае. Точки, отделяющие интервал возрастания от интервала убывания называются
точками максимума, и минимума, если они разделяют убывание от возрастания. Для
простого ответа на этот вопрос достаточно внимательно посмотреть на таблицу.
Для более детального используем численную производную ![]() ,
где Dx – приращение
аргумента и Dy – приращение
функции. Его находят как разность значений, стоящих в соседних клетках. Их
называют разностями первого порядка, а экономисты – абсолютным или цепным
приростом. Если разности положительны, то и прирост – тоже, и функция будет
возрастающей. Если разности отрицательны, то убывающей. Если прирост разделить
на время – получим скорость прироста за месяц, квартал, год, день. Это и будет
первая производная.
,
где Dx – приращение
аргумента и Dy – приращение
функции. Его находят как разность значений, стоящих в соседних клетках. Их
называют разностями первого порядка, а экономисты – абсолютным или цепным
приростом. Если разности положительны, то и прирост – тоже, и функция будет
возрастающей. Если разности отрицательны, то убывающей. Если прирост разделить
на время – получим скорость прироста за месяц, квартал, год, день. Это и будет
первая производная.
В нашем случае с января по февраль наблюдалось возрастание прибыли, с апреля по июнь – убывание, с июня по август – также незначительное возрастание, а потом – провал, хотя в декабре удалось «выйти в плюс». Наиболее удачным месяцем был февраль – максимальная прибыль, наиболее неудачным – ноябрь, где был минимум объема выпуска продукции.
4. Выпуклость и вогнутость, точки перегиба характеризуют ускорение процесса. За них отвечает вторая производная, и, следовательно, вторые конечные разности. Если первые разности оценить легко, то для вторых необходим дополнительный расчет, результаты которого желательно свести в таблицу.
Рассмотрим следующий пример, в котором будем использовать как привычные для экономистов оценки, так и численные производные.
Пример 15.6. Предприятие по плану выпускает продукцию на 600 млн. руб. в год. Плановый показатель определен как 50 млн. руб. в месяц. Фактический объем продукции составил 621,65млн. руб. Данные по факту выпускаемой продукции приведены в таблице. 1) Рассчитать процент выполнения плана по месяцам, кварталам, году. 2) Сделать вывод, какой период оказался наиболее успешным и какой – неудачным.
Решение.
В таблицу, кроме исходных данных поместим и расчетные показатели.
Таблица. Объем выпуска продукции за 20008 год.
|
Месяц |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
Итог |
|
Объемы, млн. руб. |
35,3 |
56,7 |
68,0 |
71,3 |
68,7 |
62,0 |
53,3 |
44,7 |
38 |
35 |
38,7 |
50 |
621,7 |
|
Первые разности |
21,4 |
11,3 |
3,3 |
–2,6 |
–6,7 |
–8,7 |
–8,6 |
–6,7 |
–3 |
3,7 |
12,3 |
15,7 |
|
|
Вторые разности |
–10,7 |
–7,4 |
–5,9 |
–4,1 |
–2,0 |
0,1 |
2,1 |
3,7 |
6,7 |
8,6 |
|||
|
Процент
выпол |
70,6 |
113 |
136 |
142 |
137 |
124 |
106 |
89,4 |
76 |
70 |
77,4 |
100 |
103,6 |
|
Базовый прирост |
–11,6 |
6,7 |
18 |
21,3 |
18,7 |
12 |
3,3 |
–5,3 |
–12 |
–15 |
–11 |
0 |
21,7 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.