Как и в случае одной переменной, функция двух переменных существует не при любых значениях х и у.
Определение 16.2. Совокупность пар значений (х, у), при которых
определяется функция 
,
называется областью определения или областью существования этой
функции.
Область определения наглядно иллюстрируется
геометрически, как совокупность точек, принадлежащих плоскости ХОY.
Именно она называется областью определения функции. В дальнейшем
мы будем рассматривать области, ограниченные некоторыми линиями. Эти линии
называются границами области. Точки, не лежащие на границе, называют внутренними
точками области. Область, состоящая только из внутренних точек, называется незамкнутой,
или открытой. Если к области относятся и точки границы, то ее называют замкнутой.
Область называется ограниченной, если существует такое положительное
число С, что расстояние любой точки 
плоскости
от начала координат О(0,0) меньше С, т.е. 
.
Пример 16.1. Найти область
определения функции 
.
Решение. Для того чтобы z имело действительное значение, нужно, чтобы под корнем стояло неотрицательное число, т.е. х и у должны удовлетворять неравенству
, или 
.
Все точки, удовлетворяющие этому неравенству, лежат в круге радиуса 1 с центром в начале координат и на границе этого круга (рис. 16.2).
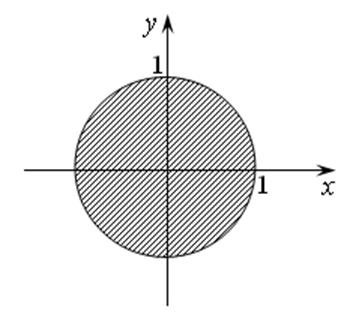
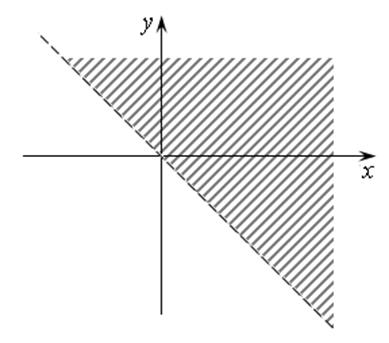
Рис. 16.2 Рис. 16.3
Пример 16.2.
Найти область определения функции 
.
РешениеТак как логарифмы определены только
для положительных чисел, то должно выполняться неравенство 
, или 
.
Ему подчиняются точки, лежащие выше прямой 
,
не включая саму прямую (рис. 16.3).
Аналогично вводятся определения функции трех, четырех
и большего числа переменных 
и области их
допустимых значений. Так, для функции трех переменных областью определения
может служить некоторое объемное тело, ограниченное или неограниченное. Для
функции четырех переменных такой геометрической интерпретации уже не
существует. В общем виде функция п переменных записывается так: 
и область ее определения находится по
общим правилам.
Рассмотрим функцию , определенную в некоторой области D
плоскости ХOY. Поскольку х и у независимые
переменные, они могут получать приращения независимо друг от друга. В
зависимости от полученных приращений 
приращения 
будут отличаться друг от друга.
Так, если переменная х получает приращение 
и становится равной 
, а переменная у остается
постоянной, то приращение функции
(16.3)
называется
частным приращением функции по переменной х и обозначается
символом 
.
Если функция получает приращение только по переменной у
, а х остается постоянным, то его называют частным приращением по
переменной у и обозначают символом 
.
(16.4)
Полное приращение функции, связанное с приращением обоих аргументов, определится из формулы
.
(16.5)
Будет ли верно равенство 
,
т.е. равна ли сумма частных приращений полному приращению функции? Рассмотрим
это на примере.
Пример
16.3. Найти полное и частные приращения функции 
при переходе от точки М(1;
2) в точку K(1,2; 2,3), если 
.
Решение.
Приращения аргументов находятся как разность значений конечной и начальной
точек: 
и 
.
Найдем все приращения по формулам (16.3 - 5):
;
;
.
Видно, что 
, т.е. полное приращение функции в
общем случае не равно сумме её частных приращений.
Понятие приращений функции тесно связано с понятием
предела функции в точке. В лекции 9 мы рассматривали предел функции одной
переменной и говорили, что число А называется пределом функции 
в точке 
,
если для любого заданного числа 
найдется такое 
, что все значения функции у
попадут в d-окрестность прямой 
,
как только аргумент х попадет в e-окрестность точки . Логично
предположить, что и предел функции двух переменных будет вводится так же, но
под e-окрестностью точки 
понимается
не интервал (
, а совокупность точек,
удовлетворяющих условию 
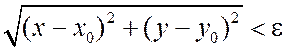и лежащих внутри круга радиуса 
с центром в точки .
Определение 16.3. Число А называется пределом функции 
при стремлении точки М к
точке 
, если для любого числа найдется такое число , что для всех точек из круга 
выполняется неравенство 
, или в символической записи:
.
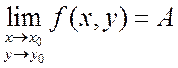Определение 16.4. Функция называется непрерывной
в точке , если она определена в этой точке, и
имеет предел, равный значению функции в этой точке, т.е.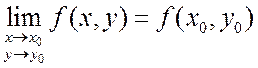 
, при стремлении к точке 
произвольным образом.
На языке приращений то же определение звучит так:
Определение 16.5. Функция называется
непрерывной в точке если бесконечно малым
приращениям аргументов соответствует бесконечно
малое приращение функции , т.е.
,
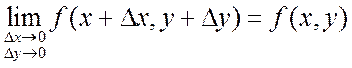или
.
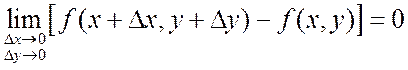Если хотя бы одно из требований этих определений не выполнено – функция называется разрывной в рассматриваемой точке, однако классификация этих разрывов сложнее, чем для функции одной переменной.
Свойства непрерывных функций одного аргумента переходят на функцию двух и большего числа переменных:
1. Если функция определена
и непрерывна в замкнутой и ограниченной области D, то внутри
этой области найдется хотя бы одна точка, в которой функция будет достигать
своего наибольшего М и наименьшего m значения
(теорема о наибольшем и наименьшем значениях).
2. Если функция определена
и непрерывна в замкнутой и ограниченной области D и если М
и m ее наибольшее и наименьшее значения, то для любого 
найдется такая точка 
, значение в которой будет равно 
(теорема о промежуточных значения).
3. Если функция определена
и непрерывна в замкнутой и ограниченной области D и
принимает как положительные так и отрицательные значения, то внутри этой
области найдется хотя бы одна точка такая, в которой функция будет равна нулю
(теорема о корнях функции).
В предыдущем параграфе мы выяснили, что функция двух переменных имеет различные частные приращения. Очевидно, что и производные функции, определяющие скорость изменения функции по разным аргументам, будут также отличаться друг от друга.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.