Теоремы о дифференцируемых функциях. Исследование поведения функции. Приложения производных к экономическим задачам. Функции многих переменных, страница 11

Определение 16.6. Частной производной по х от функции  называется предел отношения частного приращения  к приращению  при стремлении последнего к нулю.

Частная производная по х обозначается одним из символов

,          ,     .

Согласно определению

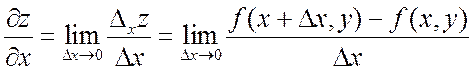.                    (16.6)

Определение 16.7. Частной производной по у от функции  называется предел отношения частного приращения  к приращению  при стремлении последнего к нулю.

Частная производная по у обозначается символами

,     ,     ,     .

Согласно определению

.                   (16.7)

Из этих определений сразу следует правило, по которому следует вычислять частную производную.

Правило вычисления частной производной. Частная производная  вычисляется от функции по переменной х в предположении, что у – постоянная. Частная производная  вычисляется по переменной у в предположении, что х – постоянная.

При вычислении частных производных работают все приемы вычислений производных сложных функций (вспомним правило цепочки).

Пример 16.4. Вычислить частные производные функции  

Решение.

 – здесь  играет роль постоянного множителя,

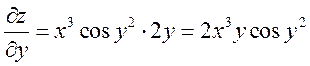 – в данном случае  числовой множитель, а производную от вычисляем «по цепочке».

Пример 16.5. Вычислить частные производные функции .

Решение.

, потому что у равен постоянной, и мы использовали формулу производной степенной функции .

, потому что , и мы используем формулу производной показательной функции .

Пример 16.6. Вычислить частные производные функции трех переменных .

Решение.

,     ,     .

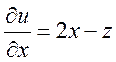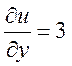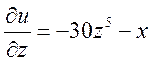Механический или кинетический смысл частных производных остается прежним: они характеризуют скорость  изменения функции по переменным х и у отдельно. С геометрией чуть сложнее. Для функции одной переменной производная численно равна тангенсу угла наклона касательной к положительному направлению оси OХ.

Для функции двух переменных касательная «переходит» в касательную плоскость к поверхности, определяемой уравнением . Любая прямая, проходящая через точку касания, и лежащая в этой плоскости, будет касательной к поверхности. Выберем из них такую, чтобы ее проекция на плоскость ХОY была параллельна оси ОХ. В этом случае у будет величиной постоянной и тангенс угла наклона этой касательной к положительному направлению оси ОХ будет равен частной производной . Если рассмотреть другую касательную, проекция которой на плоскость ХОY параллельна оси ОY, то в этом случае х будет постоянной. Тангенс угла наклона этой касательной к положительному направлению оси ОY будет равен значению частной  производной  в данной точке (рис. 16.4).

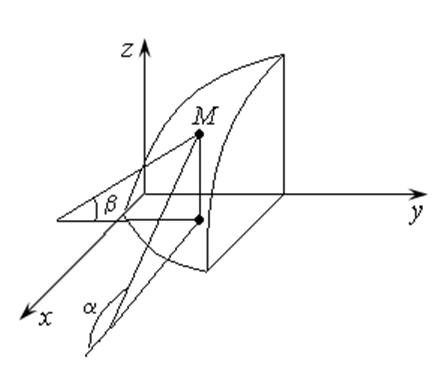
Рис. 16.4

Для функций, содержащих большее число переменных, геометрическую  интерпретацию частных производных дать нельзя.

16.5. Дифференциал

Возникает вопрос, а не существует ли одной, общей производной для функции двух или больше аргументов? Нет, не существует. Но общее изменение функции можно охарактеризовать с помощью полного дифференциала , как главной части приращения функции. Для функции одной переменной  дифференциал равен . Для функции двух переменных логично ожидать сумму «частных дифференциалов». Строгое доказательство этого утверждения можно найти в рекомендуемой литературе. Мы ограничимся определением и покажем его применение для решения задач.

Определение 16.8 . Пусть функция  непрерывна вместе со своими частными производными по х и у. Полным дифференциалом  называется сумма произведений частных производных на дифференциалы соответствующих независимых переменных, т.е.

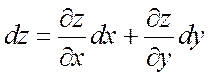.                                           (16.8)

Это выражение является аналогом формулы для дифференциала функции одной переменной. Добавлено новое слагаемое, и простая производная функции по одной переменной х заменена частными производными по х и у. Для функции трех переменных будет тройная сумма.

Напомним, что дифференциал функции приближенно равен ее приращению: . Поэтому значение функции в точке  можно определить из приближенного равенства:

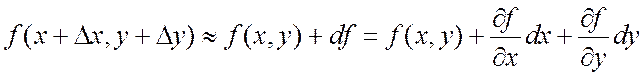,       (16.9)

где dx и dy – приращения аргументов х и у соответственно.

Пример 16.7. Найти полный дифференциал и полное приращение dz и  для функции , если , , , .

Решение.Найдем значения

(3   и   .

по таблице логарифмов или при помощи калькуляторов. Определим приращение функции

.

Найдем дифференциалы аргументов:

,   .

Тогда

,

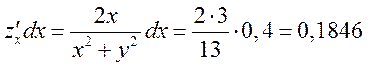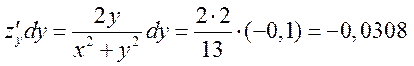
и, окончательно, получаем

.

Сравним приращение и дифференциал .

Приближенно оценим значение  по формуле (16.9):

.

Найдем относительную погрешность вычислений:

,

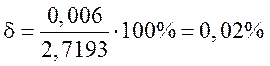что говорит о достаточной степени точности проведенных вычислений.

В разных точках функция имеет различные значения частных производных, поэтому дифференциалы будут разными. По ним можно судить о степени возрастания и убывания функции.

16.6. Градиент

Вопрос о существовании единой производной для функции двух переменных не переставал волновать пытливое человечество. Но переменные х и у не могли объединиться, поэтому задачу сформулировали по-другому: если в каждой точке функция меняется по двум и больше аргументам, то в каком направлении ее изменение будет наибольшим?

Направление, как известно, задается вектором. В общем виде вектор может быть записан так:, где  – координаты вектора в декартовом базисе, |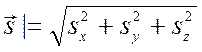 – модуль  вектора,

,    ,   

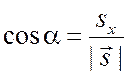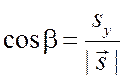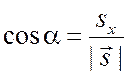
– направляющие косинусы, сумма их квадратов равна единице. Это координаты единичного направляющего вектора  для вектора . Его употребляют в вычислениях, когда важно именно направление, а не длина вектора.

Пусть функция  непрерывна вместе со своими частными производными в некоторой области D и точке , принадлежит этой функции. Проведем из точки М вектор . Выражение вида

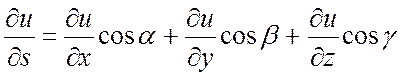                          (16.10)

называется производной функции  в направлении вектора . Она позволяет найти скорость изменения данной функции в направлении вектора .

Рассмотрим вектор, координаты которого равны частным производным  функции  в некоторой точке . Этот вектор называется градиентом функции  в данной точке.

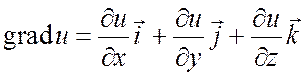.                                 (16.11)