Теоремы о дифференцируемых функциях. Исследование поведения функции. Приложения производных к экономическим задачам. Функции многих переменных, страница 7

ПРИЛОЖЕНИЯ ПРОИЗВОДНЫХ К ЭКОНОМИЧЕСКИМ ЗАДАЧАМ

Ни одно человеческое исследование не может называться наукой, если оно не прошло через математические
доказательства.

Леонардо да Винчи

ПЛАН

1.  Экономический смысл производной.

2.  Эластичность. Задача о спросе и предложении

3.  Применение производной для функции, заданной таблично.

15.1. Экономический смысл производной

Рассмотрим задачу, иллюстрирующую экономический смысл производной. Издержки производства y будем рассматривать как функцию количества выпускаемой продукции x. Пусть Dx – прирост продукции, тогда Dy – приращение издержек производства. Воспользуемся формулой (11.12)

Если , то получим

.

Таким образом, производная  характеризует приближенно дополнительные затраты на производство единицы дополнительной продукции и выражает предельные издержки производства.

Аналогичным образом, могут быть определены предельные выручка, предельный продукт и другие предельные показатели. Предельные величины характеризуют не состояние (как суммарная или средняя величина), а процесс, изменение экономического объекта.

Пример 15.1. Функция издержек производства продукции некоторой фирмы имеет вид

.

Найти средние и предельные издержки и вычислить их значение при .

Решение. Найдем производную  и ее значение  – предельные издержки производства:

,          .

Средние издержки:

,    .

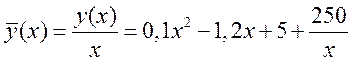Это означает, что при данном уровне производства (количестве выпускаемой продукции) средние затраты на производство одной единицы продукции составляют 28 ден. ед., а увеличение объема производства на одну единицу продукции обойдутся фирме приближенно в 11 ден. ед.

15.2. Эластичность. Задача спроса и предложения

 Для исследования экономических процессов и решения других прикладных задач часто используется понятие эластичности.

Определение 15.1. Эластичностью функции  называется предел отношения относительного приращения функции y(x) к относительному приращению переменной xпри :

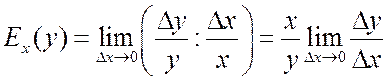.                           (15.1)

Вспоминая определение производной, получим

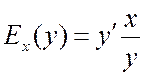.                                                (15.2)

Эластичность функции показывает приближенно, на сколько процентов изменится функция  при увеличении независимой переменной на 1%.

Отметим, что эластичность можно представить в виде

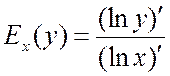.                                                (15.3)

В связи с этим становятся понятными следующие свойства эластичности:

,      .

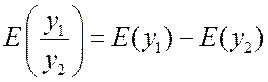Пример 15.2. Найти эластичность функций: а) , б) .

Решение. а) Поскольку , то по формуле (15.2) получаем

.

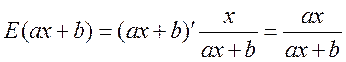б) Для степенной функции

.

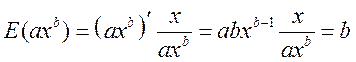Как мы видим, эластичность степенной функции есть величина постоянная, равная показателю степени. Это характерное свойство только степенных функций. Поэтому степенные функции довольно часто используются в экономической теории, т.к. все ее параметры имеют четкий экономический смысл.

В случае табличного задания функции определение эластичности не однозначно. Это связано с тем, что в отношении  не ясно, что брать в качестве x: первоначальное значение x₁, конечное значение x₂ или среднее значение . В зависимости от этого различают:

конечную эластичность

,

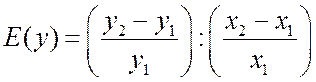среднюю эластичность

,

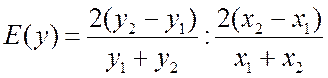а также логарифмическую эластичность

.

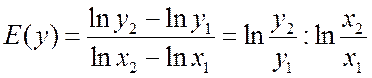Все эти выражения мало отличаются друг от друга при небольших относительных изменениях величин x и y.

Эластичность функций часто применяется при анализе спроса и потребления. Например, эластичность спроса y относительно цены x (или дохода x) показывает, на сколько процентов изменится спрос (объем потребления) при увеличении цены (или дохода) на 1%. Спрос называется эластичным, если , неэластичным, если , и нейтральным, если .

Пример 15.3. Зависимость между себестоимостью единицы продукции y (тыс. руб.) и выпуском продукции x (млн. руб.) выражается функцией

.

Найти эластичность себестоимости при выпуске продукции, равном 60 млн. руб.

Решение. Воспользуемся решением предыдущей задачи

.

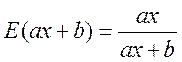В нашем случае

.

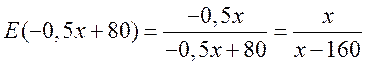При

,

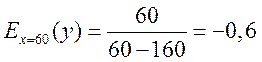т.е. при выпуске продукции, равном 60 млн. руб., увеличение его на 1% приведет к снижению себестоимости на 0,5%.

Пример 15.4. Функция спроса и предложения имеют соответственно вид:

,   ,

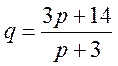где q и s – количество товара, соответственно покупаемого и продаваемого в единицу времени, p – цена единицы товара. Найти: а) равновесную цену, т.е. цену, при которой спрос и предложения уравновешиваются; б) эластичности спроса и предложения при равновесной цене; в) изменение дохода при увеличении цены на 10% от равновесной.

Решение. а) Равновесная цена определяется из условия , т.е.

,

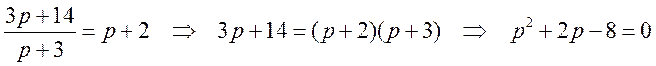откуда находим  и . Последний корень отбрасываем, т.к. цена не может быть отрицательной и устанавливаем, что равновесная цена равна 2 ден. ед.

б) Найдем эластичности спроса и предложения. Вычисляем соответствующие производные:

,   ,

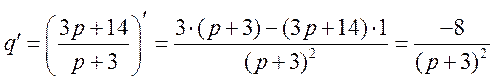и подставляем их в формулу (15.2):

,

.

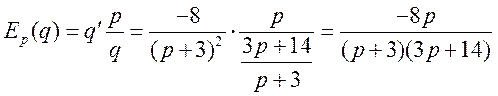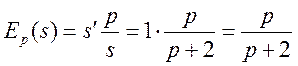Для равновесной цены  имеем

,   .

Так как полученные значения эластичностей меньше 1, то спрос и предложение данного товара при равновесной (рыночной) цене неэластичны относительно цены. Это означает, что изменение цен не приведет к резкому изменению спроса и предложения.

в) При увеличении цены p на 10% от равновесной цены спрос уменьшится на , следовательно, доход  от проданной продукции (цена p умноженная на количество q проданного товара) возрастет в целом на . Несмотря на то, что цена на товар увеличилась и спрос на нее упал, предприятие все равно получает прибыль.

Пример 15.5. Зависимость между спросом и ценой q и ценой p за единицу продукции, выпускаемой некоторым предприятием, дается соотношением:

.

Найти эластичность спроса. Выяснить, при каких значениях цен спрос является эластичным, нейтральным и неэластичным. Какие рекомендации о цене за единицу продукции можно дать руководителям предприятия при  и при  ден. ед.?

Решение. Найдем эластичность по формуле (15.2):

.

Для нахождения p воспользуемся тем, что при нейтральном спросе , т.е.

.

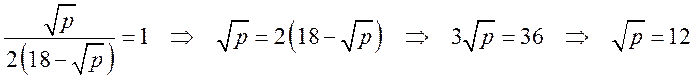Тогда .

Далее, принимая во внимание, что цена  и спрос , получим еще одно ограничение на p:

.

Таким образом, область изменения цены p  интервал (0; 324). Причем он  точкой p = 144 делится на две части. Посмотрим модуль эластичности на каждой из них.