Сравнение этих формул показывает, что производная в
данной точке по направлению вектора ![]() имеет
наибольшее значение, если направление вектора
имеет
наибольшее значение, если направление вектора ![]() совпадает с направлением градиента. Это наибольшее
значение производной равно модулю градиента в данной точке. Поэтому вектор
градиент показывает направление наибольшего возрастания функции в данной точке,
а его модуль – скорость наибольшего возрастания.
совпадает с направлением градиента. Это наибольшее
значение производной равно модулю градиента в данной точке. Поэтому вектор
градиент показывает направление наибольшего возрастания функции в данной точке,
а его модуль – скорость наибольшего возрастания.
Пример
16.8. Дана функция ![]() .
Найти производную
.
Найти производную ![]() в точке
в точке
М(1, 1, 1) в направлении вектора ![]() и вектора градиента. Сравнить
скорости изменения функции в этих направлениях.
и вектора градиента. Сравнить
скорости изменения функции в этих направлениях.
Решение.Для того, что бы найти производную в направлении вектора, найдем вначале его модуль и направляющие косинусы.
![]() ,
, 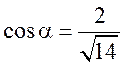 ,
, 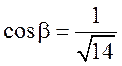 ,
,  .
.
Найдем частные производные данной
функции в точке ![]() :
:
![]() ,
, ![]() ,
,
![]() .
.
Производная функции в направлении
вектора ![]() :
:
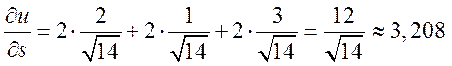 .
.
Составим вектор градиент по найденным частным производным в точке М и найдем его модуль:
![]() ,
,
![]() ,
,
что и следовало ожидать.
Если функция ![]() есть
функция двух переменных, то вектор
есть
функция двух переменных, то вектор
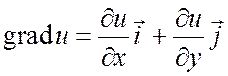
в
точке ![]() лежит в плоскости ХОY
и перпендикулярен проекции сечения поверхности плоскостью
лежит в плоскости ХОY
и перпендикулярен проекции сечения поверхности плоскостью ![]() , параллельной плоскости ХОY.
(рис. 16.5).
, параллельной плоскости ХОY.
(рис. 16.5).
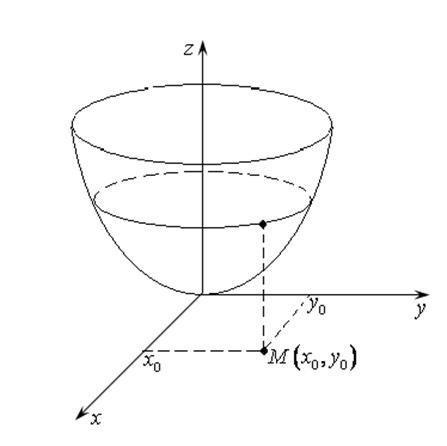

Рис. 16.5
Сделаем первые выводы по этой теме.
1. Закон изменения одной переменной U в зависимости от двух и более независимых друг от друга переменных х, у и т.д. называется функцией многих переменных.
2. Изменения U по разным переменным различаются друг от друга и характеризуются частными производными. Частные производные показывают скорость изменения в своем направлении.
3. Скорость изменения в произвольном направлении
характеризуется производной по направлению вектора ![]() .
.
4. Направление, в котором скорость имеет наибольшее значение, задается вектором, имеющим специальное название градиент. Его координаты равны значению частных производных в данной точке, а модуль – скорости изменения.
ПЛАН
8. Введение.
9. Частные производные высших порядков.
10. Экстремумы функции двух переменных.
11. Наибольшее и наименьшее значение функции в замкнутой области.
12. Подбор параметров для эмпирических формул простейшего вида по методу наименьших квадратов
13. Заключение.
При изучении функции одной переменной кроме производной первого порядка, характеризующей скорость изменения какого-либо процесса, мы ввели понятие второй производной, которая отвечала за ускорение. У функции двух переменных существует две частные производные, которые в общем случае также являются функциями тех же переменных, и, следовательно, их снова можно дифференцировать и по х, и по у. Покажем, как это делается.
Пусть функция z = f(x,y)
непрерывна вместе со своими частными производными ![]() и
и
![]() в некоторой области D
плоскости ХОY.
в некоторой области D
плоскости ХОY.
Определение 17.1. Частными производными второго порядка (или вторыми частными производными) называются
производные от производных ![]() и
и ![]() .
.
Вторые частные производные обозначаются так:
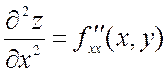 ,
,
здесь функция последовательно дифференцируется по х дважды;
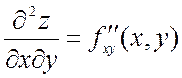 ,
,
здесь f дифференцируется сначала по х, а потом результат по у;
 ,
,
здесь f дифференцируется сначала по у, а потом результат по х;
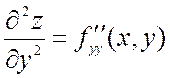 ,
,
здесь f дифференцируется дважды по у.
Первая и последняя производные называются иногда чистыми, а вторая и третья – смешанными производными второго порядка.
Можно доказать (см. учебник Кремера)), что
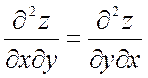 ,
,
при условии непрерывности этих производных в заданных точках, т. е. вторая смешанная производная не зависит от порядка дифференцирования и поэтому четыре частных производных сводятся к трем.
Производные второго порядка можно вновь дифференцировать как по х, так и по у. Получим производные третьего порядка, две из которых чистые, а остальные шесть – смешанные:
![]() ,
, 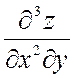 ,
, 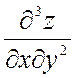 ,
,
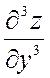 .
.
Здесь мы учли, что
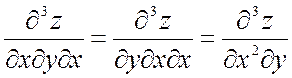 и
и 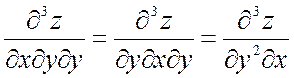 ,
,
и поэтому восемь частных производных сводятся к четырем.
Этот процесс можно продолжить и получить производные любого порядка, при условии, что все они непрерывны в заданной точке.
Пример 17.1.
Вычислить производные второго порядка от функции ![]()
Решение. Найдем производные первого порядка, учитывая, что частная производная по х вычисляется в предположении, что у – постоянная и наоборот:
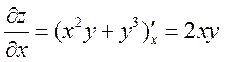 ,
, 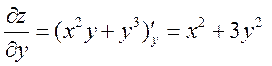 .
.
Найдем производные второго порядка:
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Пример
17.2. Дана функция ![]() . Показать, что
. Показать, что ![]() .
.
Решение. Найдем последовательно значения всех производных и проверим данное равенство.
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Подставим найденные значения в исходное равенство:
![]() .
.
Мы видим, что равенство ![]() для заданной функции выполняется.
для заданной функции выполняется.
Пример
17.3. Дана функция 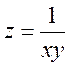 . Показать, что
. Показать, что ![]() .
.
Решение.
 ,
,  ,
,
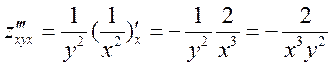
– это левая часть равенства.
Для вычисления правой учтем, что ![]() уже известно, и найдем
уже известно, и найдем
 ,
, 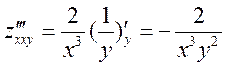 .
.
Т.о. исходное равенство для заданной функции.
Как видно из приведенных примеров, следует соблюдать бдительность и отделять по возможности те переменные, которые в данном случае играют роль постоянной.
Мы достаточно подробно обсуждали экстремумы функции одной переменной. Перенесем эти знания на функции двух переменных.
Определение 17.2. Точка ![]() называется
точкой максимума функции
называется
точкой максимума функции ![]() , если
, если
![]()
для
всех точек (х,у), достаточно близких к точке ![]() и отличных от нее (рис. 17.1).
и отличных от нее (рис. 17.1).
Определение 17.2. Точка ![]() называется
точкой минимума функции
называется
точкой минимума функции ![]() , если
, если
![]()
для
всех точек (х,у), достаточно близких к точке ![]() и
отличных от нее. (рис. 17.2).
и
отличных от нее. (рис. 17.2).
Точки, в которых частные производные равны нулю или не существуют, называются критическими.
Иногда точку экстремума и ее характер можно определить из соображений здравого смысла.
Например, функция ![]() имеет
минимум при
имеет
минимум при ![]() и
и ![]() ,
т.е. в точке М(1,2). Действительно, для любых
,
т.е. в точке М(1,2). Действительно, для любых ![]() первое
слагаемое будет расти, и для
первое
слагаемое будет расти, и для ![]() – тоже, поэтому в
точке М(1,2) функция имеет минимум, причем
– тоже, поэтому в
точке М(1,2) функция имеет минимум, причем ![]() (рис.
17.1).
(рис.
17.1).
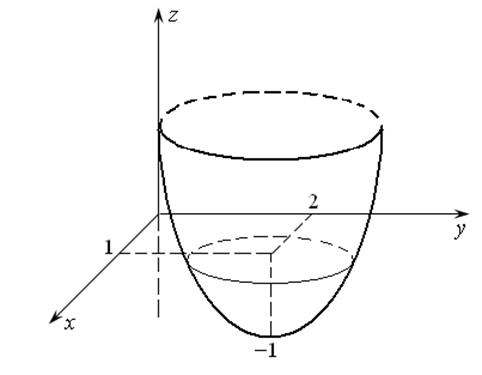

Рис. 17.1 Рис. 17.2
Функция 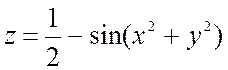 имеет максимум в
точке (0,0), причем
имеет максимум в
точке (0,0), причем 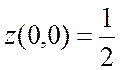 (рис. 17.2).
(рис. 17.2).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.