ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ЭКОНОМИКИ И УПРАВЛЕНИЯ
Методические указания
по выполнению индивидуального домашнего задания
Методические указания рассмотрены и утверждены на заседании кафедры экономико-математических методов и прогнозирования от ……… 2005 г., протокол №
Составитель: ст. преподаватель Е.С. Федоткина
2.1. Задача о перевозке груза (транспортная задача) ........ 6
2.2 Задача о распределении механизмов между участками ...................................................................................................... 18
2.3. Задача о назначении напарников ............................... 23
Литература ................................................................................. 32
Выполнение задания «Решение задач линейного программирования транспортного типа» предназначено для более глубокого усвоения материала темы «Транспортная задача», развития навыков экономико-математического моделирования и практического решения задач транспортного типа студентами НГУЭУ, изучающими дисциплину «Экономико-математические методы».
Методические указания содержат краткое описание экономико-математической модели транспортной задачи и ее свойств, а также изложение методов решения различных задач транспортного типа. Для каждой задачи используется своя нумерация формул и таблиц.
Каждый студент получает свой вариант задания, содержащий три задачи. Требования к выполнению и оформлению задания стандартные: работа должна содержать описание ситуации, подробное решение с пояснениями действий и полный ответ в конце решения каждой из задач.
Описание ситуации. Некоторый однородный продукт (груз) сосредоточен в m пунктах отправления (производства) в количествах а1, а2, …, am единиц соответственно. Его нужно доставить в n пунктов назначения (потребления), подавших заявки на этот продукт в количествах b1, b2, …, bn единиц соответственно. Предполагается, что сумма всех заявок равна сумме всех запасов, т.е. выполнено следующее условие:
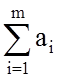 =
=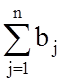 . (1)
. (1)
Это условие гарантирует, что все заявки будут выполнены полностью и из каждого пункта отправления будет вывезен весь груз.
Известны тарифы (стоимости) cij (![]() ) перевозки единицы груза из i‑го пункта отправления в j-й пункт
назначения. Требуется найти план перевозок, который удовлетворяет заявки всех
пунктов назначения и минимизирует суммарные затраты на перевозку.
) перевозки единицы груза из i‑го пункта отправления в j-й пункт
назначения. Требуется найти план перевозок, который удовлетворяет заявки всех
пунктов назначения и минимизирует суммарные затраты на перевозку.
Математическая модель. Для построения модели описанной выше
ситуации, определим переменные xij —
количество груза, перевозимого из i-го пункта отправления
в j-й пункт назначения (![]() ). Ясно, что они должны
принимать неотрицательные значения. Множество всех переменных (план перевозок)
задается в виде матрицы X = (xij), имеющей размеры mхn.
). Ясно, что они должны
принимать неотрицательные значения. Множество всех переменных (план перевозок)
задается в виде матрицы X = (xij), имеющей размеры mхn.
Сама математическая модель задачи нахождения плана перевозок с наименьшими суммарными затратами выглядит так:
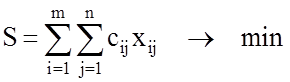 , (2)
, (2)
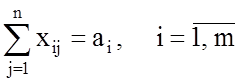 , (3)
, (3)
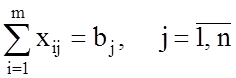 , (4)
, (4)
![]() . (5)
. (5)
Формула (2) задает правило подсчета общих транспортных затрат S, необходимых для реализации плана перевозок X = (xij). Таким образом, S является целевой функцией, и решается задача ее минимизации на множестве планов перевозок, задаваемом ограничениями модели (3) – (5).
Условие (3) показывает, что общее количество груза, вывезенное из любого пункта отправления должно равняться величине запаса этого пункта. Условие (4) показывает, что общее количество груза, доставленное в любой пункт назначения должно равняться потребности этого пункта.
Задача (2) – (5) называется транспортной задачей, а равенства (3) – (4) называются условиями сбалансированности плана перевозок X = (xij).
План перевозок X = (xij) (![]() ), удовлетворяющий
соотношениям (3) – (5),
называется допустимым планом задачи (2) – (5).
), удовлетворяющий
соотношениям (3) – (5),
называется допустимым планом задачи (2) – (5).
Допустимый план X* = (![]() ) называется оптимальным
планом, если
на нем общая величина затрат на перевозки S(X*) минимальна.
) называется оптимальным
планом, если
на нем общая величина затрат на перевозки S(X*) минимальна.
Транспортная задача называется закрытой (сбалансированной),если выполнено условие (1). Это условие обеспечивает существование оптимального решения задачи (2) – (5).
Теорема 1. Транспортная задача имеет оптимальный план тогда и только тогда, когда она является закрытой.
Если условие (1) не выполнено, то транспортная задача называется открытой. В этом случае ее можно свести к закрытой задаче путем введения фиктивного пункта отправления или назначения (см. решение задачи 1).
Допустимый план транспортной задачи называется опорным планом, если столбцы матрицы условий, соответствующие его положительным компонентам, линейно независимы. Известно, что максимальное число линейно независимых столбцов матрицы условий транспортной задачи равно m + n – 1. Поэтому опорный план не может иметь более m + n – 1положительных компонент. Если опорный план имеет ровно m + n – 1положительных компонент, то он называется невырожденным планом, а если меньше, то вырожденным.
Транспортная задача является задачей линейного программирования, но она имеет ряд особенностей, отличающих ее от других задач этого типа:
· все ее общие ограничения задаются в виде равенств;
· все коэффициенты при переменных в ограничениях равны 1;
· каждая переменная входит только в два ограничения.
Поэтому для решения транспортной задачи используются методы, учитывающие ее специфику. Стандартный метод ее решения включает следующие пункты:
1. построение начального опорного плана перевозок;
2. проверка полученного плана на оптимальность. Если он не является оптимальным, то строится новый улучшенный план перевозок, на котором транспортные затраты меньше, или, по крайней мере, равны затратам предыдущего плана. Этот пункт повторяется до тех пор, пока не будет получено оптимальное решение.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.