Уральский государственный технический университет
«Анализ линейной модели на чувствительность»
вариант №13
Студенты: Печерский С.И.
Плотников А.А.
Преподаватель: Черногородова Г.М.
Екатеринбург
2002
Лабораторная работа
№1
Анализ линейной модели на чувствительность
1. Решение исходной задачи.
Запишем условие исходной задачи в канонической форме (Таблица 1).
|
A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
b |
C |
|
-4 |
5 |
1 |
0 |
0 |
0 |
20 |
-2 |
|
-2 |
-1 |
0 |
1 |
0 |
0 |
-6 |
3 |
|
5 |
-1 |
0 |
0 |
1 |
0 |
45 |
0 |
|
1 |
-1 |
0 |
0 |
0 |
1 |
6 |
0 |
Решим задачу линейного программирования (ЛП) симплекс-методом .
Начальная симплекс-таблица (Таблица 2).
|
Bx |
Cj |
A0 |
A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
|
A3 |
0 |
20 |
-4 |
5 |
1 |
0 |
0 |
0 |
|
A4 |
0 |
-6 |
-2 |
-1 |
0 |
1 |
0 |
0 |
|
A5 |
0 |
45 |
5 |
-1 |
0 |
0 |
1 |
0 |
|
A6 |
0 |
6 |
1 |
-1 |
0 |
0 |
0 |
1 |
|
D |
0 |
2 |
-3 |
0 |
0 |
0 |
0 |
Последняя симплекс-таблица (Таблица 3).
|
Bx |
Cj |
A0 |
A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
|
А2 |
3 |
40/3 |
0 |
1 |
0.238 |
0 |
0.190 |
0 |
|
А4 |
0 |
92/3 |
0 |
0 |
0.333 |
1 |
0.667 |
0 |
|
А1 |
-2 |
35/3 |
1 |
0 |
0.048 |
0 |
0.238 |
0 |
|
А6 |
0 |
23/3 |
0 |
0 |
0.190 |
0 |
-0.048 |
1 |
|
D |
50/3 |
0 |
0 |
0.619 |
0 |
0.095 |
0 |
Запишем полученное оптимальное решение х0=(35/3,40/3) при оптимальном базисе Вх0=(А2,А4,А1,А6). При этом значение целевой функции z=-50/3.
2. Проведём анализ изменения коэффициента целевой функции при базисной переменной С1 (Таблица 4).
|
DС1, % |
C1 |
X10 |
X20 |
z |
Dz, % |
|
+50% |
-1 |
35/3 |
40/3 |
-85/3 |
-70% |
|
+40% |
-1.2 |
35/3 |
40/3 |
-26 |
-56% |
|
+30% |
-1.4 |
35/3 |
40/3 |
-71/3 |
-42% |
|
+20% |
-1.6 |
35/3 |
40/3 |
-64/3 |
-28% |
|
+10% |
-1.8 |
35/3 |
40/3 |
-19 |
-14% |
|
-10% |
-2.2 |
35/3 |
40/3 |
-43/3 |
+14% |
|
-20% |
-2.4 |
35/3 |
40/3 |
-12 |
+28% |
При уменьшении С1 на 30% оптимальный базис не сохраняется, происходит переход к новому оптимальному решению xo=(0.714;4.571) в базисе Вх0=(A2,A5,A1,A6).
При увеличении С1 на 50% (с шагом 10%) оптимальный базис Вх0=(А2,А4,А1,А6) сохраняется.
3. Изменение коэффициентов при небазисных переменных не влияет на оптимальное решение и значение целевой функции.
4. Проведём изменение b3, результаты сведём в таблицу (см. таблицу 8).
Таблица 8
|
Db3, % |
b3 |
X10 |
X20 |
z |
Dz, % |
|
-50% |
22.5 |
6.310 |
9.048 |
-14.524 |
+12.86% |
|
-40% |
27.0 |
7.381 |
9.905 |
-14.952 |
+10.29% |
|
-30% |
31.5 |
8.452 |
10.762 |
-15.381 |
+7.72% |
|
-20% |
36.0 |
9.524 |
11.619 |
-15.810 |
+5.14% |
|
-10% |
40.5 |
10.600 |
12.480 |
-16.238 |
+2.57% |
|
0% |
45.0 |
11.667 |
13.333 |
-16.667 |
0% |
|
10% |
49.5 |
12.738 |
14.190 |
-17.095 |
-2.57% |
|
20% |
54.0 |
13.810 |
15.048 |
-17.524 |
-5.14% |
|
30% |
58.5 |
14.881 |
15.905 |
-17.952 |
-7.71% |
|
40% |
63.0 |
15.952 |
16.762 |
-18.381 |
-10.28% |
|
50% |
67.5 |
17.024 |
17.619 |
-18.810 |
-12.86% |
При изменении b3 в пределах ±50% (с шагом 10%) оптимальный базис Вх0=(А2,А4,А1,А6) сохраняется, но оптимальное решение и значение оптимальной функции меняются.
5. Анализ изменения столбца матрицы ограничений А при базисной переменной х1 (Таблица 9).
Таблица 9
|
DА1, % |
А11 |
А12 |
А13 |
А14 |
X10 |
X20 |
z |
Dz, % |
|
-15% |
-4.60 |
-2.30 |
4.25 |
0.85 |
14.715 |
17.538 |
-23.183 |
-39.10% |
|
-10% |
-4.40 |
-2.20 |
4.50 |
0.90 |
13.536 |
15.912 |
-20.663 |
-23.98% |
|
-5% |
-4.20 |
-2.10 |
4.75 |
0.95 |
12.532 |
14.527 |
-18.517 |
-11.10% |
|
0% |
-4.00 |
-2.00 |
5.00 |
1.00 |
11.667 |
13.333 |
-16.667 |
0.00% |
При уменьшении коэффициентов на 20% попадаем в область оптимального решения xo=(16.118;19.474) в базисе Вх0=(A1,A6,A2,A4).
При увеличении коэффициентов на 5% попадаем в область оптимального решения xo=(10.913;12.294) в базисе Вх0=(A6,A4,A2,A1).
6. Введем дополнительные ограничения. Для этого решим исходную задачу ЛП, используя геометрическую интерпретацию (смотри рис. 1).
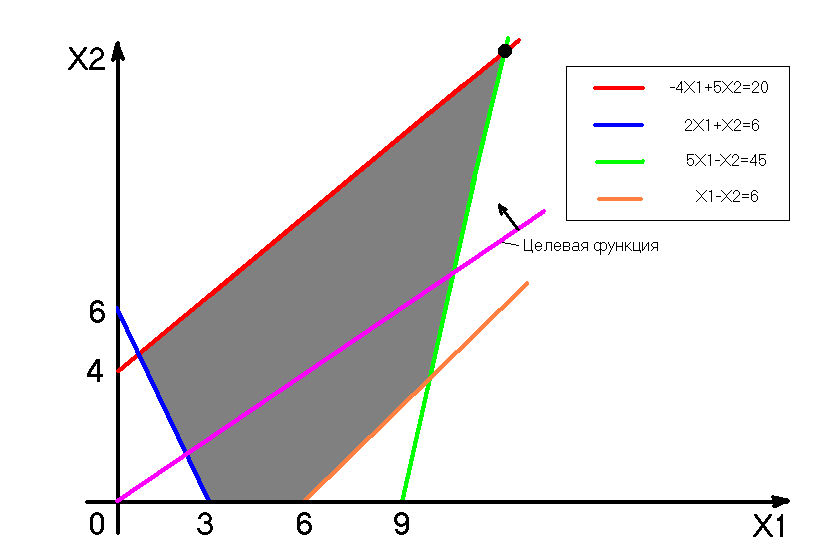
Рис. 1. Решение исходной задачи ЛП с помощью геометрической интерпретации
7.1 Прямое ограничение Х1£9 (смотри рис. 2). Его введение повлекло за собой изменение значения целевой функции и оптимального решения: Z=-15.6, X10=9, X20=11.2
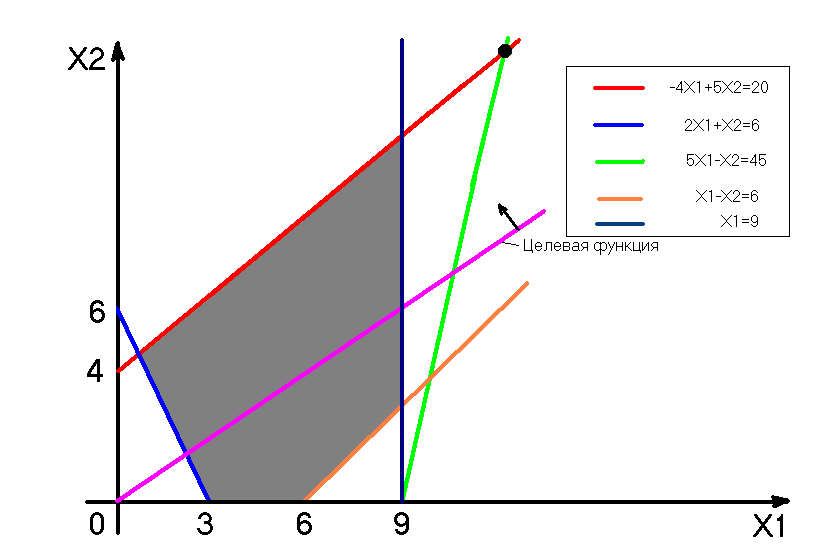
Рис. 2. Добавление прямого ограничения Х1£9
7.2 Непрямое ограничение 0.667X1+X2>=6 (смотри рис. 3). Его введение в данном случае не повлекло за собой изменение значения целевой функции и оптимального решения: Z=-50/3, X10=35/3, X20=40/3.
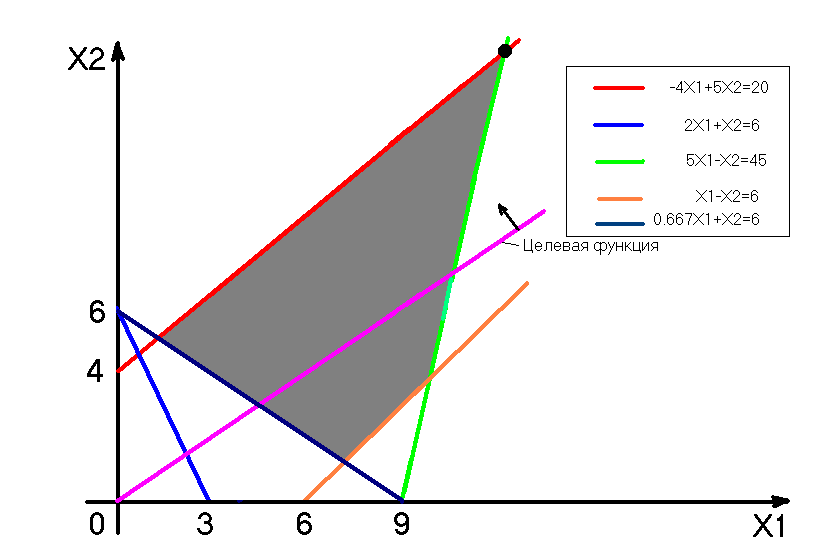
Рис. 3. Добавление непрямого ограничения 0.667X1+X2>=6
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.