Решение задач линейного программирования транспортного типа: Методические указания к выполнению индивидуальных домашних заданий, страница 9

Считается, что количество неустраненных правонарушений (стоимость назначения) c_ij зависит от того, как составлена пара (i, j). Отсюда постановка цели задачи: найти оптимальные пары из опытного и молодого сотрудников для работы в патруле, чтобы общее количество неустраненных правонарушений было минимальным.

Экономико-математическая модель задачи о назначении напарников имеет вид:

                               x₁₁ + x₁₂ + x₁₃ + x₁₄ = 1,                                                      (3.1)

                               x₂₁ + x₂₂ + x₂₃ + x₂₄ = 1,                                                         (3.2)

                               x₃₁ + x₃₂ + x₃₃ + x₃₄ = 1,                                                      (3.3)

                               x₄₁ + x₄₂ + x₄₃ + x₄₄ = 1,                                                      (3.4)

                               x₁₁ + x₂₁ + x₃₁ + x₄₁ = 1,                                                      (3.5)

                               x₁₂ + x₂₂ + x₃₂ + x₄₂ = 1,                                                       (3.6)

                               x₁₃ + x₂₃ + x₃₃ + x₄₃ = 1,                                                      (3.7)

                               x₁₄ + x₂₄ + x₃₄ + x₄₄ = 1,                                                       (3.8)

                                 x_ij  0,        i, j = ,                                                       (3.9)

        S = 2x₁₁ + 10x₁₂ + 9x₁₃  + 7x₁₄  +  15x₂₁ +  4x₂₂ + 14x₂₃  + 8x₂₄ + 13x₃₁ +

                     14x₃₂ + 16x₃₃  + 11x₃₄ + 4x₄₁ + 15x₄₂ + 13x₄₃  + 19x₄₄  min.            (3.10)

Эту модель можно рассматривать как транспортную задачу, содержащую четыре пункта производства (опытные сотрудники) с объёмами предложений a_i = 1, (i = ), четыре пункта потребления (молодые сотрудники) с заявками b_j = 1, (j = ) и транспортные тарифы (количество правонарушений или «стоимость назначения») с_ij (i = , j = ).

Таким образом, построенная модель является специальным случаем транспортной задачи: m = n = 4 и a_i = b_j = 1 для всех i, j. Так как 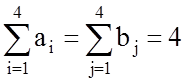, то рассматриваемая задача является закрытой. Для ее решения можно использовать рассмотренные выше методы.

3.1. Начальный опорный план Х₀ находим методом северо-западного угла (см. табл. 3.0), который был подробно разобран при решении задачи 1.

Таблица 3.0

bj ai	К 1	М 1	В 1	Ю 1
И   1	2 1	10 0	9	7
П   1	15	4   1	14   0	8
С   1	13	14	16    1	11   0
Е   1	4	15	13	19    1

Получено 4 занятых клетки. План X₀ является вырожденным, поскольку занятых клеток в опорном плане должно быть: m + n – 1 = 4 + 4 – 1 = 7. Значит, следует три занятые клетки плана сделать условно-занятыми путем заполнения их нулями. Лучше эту процедуру провести следующим образом: заполняется нулем клетка рядом с занятой клеткой по строке или ниже занятой клетки по столбцу.

Значение целевой функции на этом плане

S₀ = 2  1 + 4  1 + 16  1 + 19  1 = 41.

 

            1  0  –  –

 Х₀ =    –  1  0 –     ,       S₀ = 41.

            –  –  1  0

            –  –  –  1

3.2. Для нахождения оптимального решения используем метод потенциалов.

Шаг 1. Проверим начальный опорный план X₀  на оптимальность. Используем критерий оптимальности плана (см. стр. 6) для задачи (3.1) – (3.10). Найдем потенциалы строк U_i и столбцов V_j (см. табл. 3.1).

Пусть исходное значение U₁ = 10.

                       V₁ = U₁ + С₁₁ = 10 + 2 = 12,

                       V₂ = U₁ + С₁₂ = 10 + 10 = 20,

                       U₂ = V₂ – С₂₂ = 20 – 4 = 16,

                       V₃ = U₂ + С₂₃ = 16 + 14 = 30,

                       U₃ = V₃ – С₃₃ = 30 – 16 = 14,

                       V₄ = U₃ + С₃₄ = 14 + 11 = 25,

                       U₄ = V₄ – С₄₄ = 25 – 19 = 6.

Проверим выполнение соотношения

∆_ij  = V_j – U_i – С_ij  0

для свободных клеток плана. Выпишем только ∆_ij > 0.

                                                ∆₄₁ = 12 – 6 – 4 = 2,

                                                ∆₁₃ = 30 – 10 – 9 = 11,

                                                ∆₄₃ = 30 – 6 – 13 = 11,

                                                ∆₁₄ = 25 – 10 – 7 = 8,

                                                ∆₂₄ = 25 – 16 – 1 = 1.

Таблица 3.1

bj ai	К 1	М 1	В 1	Ю 1	Ui
И     1	2     1	10    0  –	9     +	7	10
П     1	15	4  1    +	14 0      –	8	16
С     1	13	14	16      1	11     0	14
Е     1	4	15	13	19     1	6
Vj	12	20	30	25	S0 = 41

Выбираем максимальные положительные значения ∆₁₃ = ∆₄₃ = 11, которые соответствуют разным свободным клеткам. Для последующих действий следует взять клетку (1, 3) с меньшими затратами, так как c₁₃ < c₄₃ (9 < 13).

Улучшение плана в таблице 3.1 проводится следующим образом. К свободной клетке (1, 3), которая считается исходной и отмечается знаком «+», составляется замкнутый цикл. В него включаются клетки (1, 3), (2, 3), (2, 2), (1, 2). Вершины цикла отмечаются чередующимися знаками «+» и «–». Из минусовых клеток (2, 3) и (1, 2) выбирается минимальное значение: θ = min{x₂₃, x₁₂} = min{0, 0} = 0.

Обе клетки (2, 3) и (1, 2) содержат нули, однако освобождается клетка (2, 3) с большим значением тарифа: c₂₃ < c₁₂ (14 < 10). Корректирующая величина θ = 0 помещается в свободную клетку (1, 3). К значению в клетке (2, 2) прибавляется нуль, а от значения в клетке (1, 2) отнимается нуль.

В действительности улучшения значения целевой функции не произойдёт, так как по циклу перемещается θ = 0. Однако изменится расположение занятых и свободных клеток в транспортной таблице. Значение целевой функции останется прежним:

S₁ = S₀  –  ∆₁₃ ×θ  = 41 –  110 = 41.