Решение задач линейного программирования транспортного типа: Методические указания к выполнению индивидуальных домашних заданий, страница 6

Производится перераспределение поставок по циклу: клетка (1, 4) становится занятой поставкой в 5 единиц, а клетка (4, 4) становится свободной. К поставкам в плюсовых клетках прибавляется величина θ, равная 5, а от поставок в минусовых клетках отнимается эта величина. В результате в таблице 1.4 получен новый опорный план X₂:

                                       68   45   –     5   –                 

                           X₂ =      –     –   18    –   –    ,    S₂ = S₁ – ∆₁₄×θ = 3622 – 5×5 = 3597.

                                   –     –   72   26  87

                                   –    23   –     –

Шаг 3. Проведем анализ нового опорного плана X₂. Для нового опорного плана рассчитываем потенциалы U_i и V_j. Максимальные положительные значения ∆_ij = 4 соответствуют двум клеткам: (3, 2) и (2, 5). Выбираем клетку с минимальным значением тарифа, т.е. клетку (2,5). К ней составляется цикл, по которому происходит пересчет поставок. Он включает клетки (2,5), (4, 5), (4, 2), (1, 2), (1, 4), (3, 4), (3, 3) и (2, 3). Выберем θ = min{x₄₅, x₁₂, x₃₄, x₂₃} = min{87, 45, 26, 18} = 18.

В результате корректировки получен новый опорный план Х₃ (см. табл. 1.5).

                                    68   27    –   23   –                   

                         X₃ =     –     –     –    –   18    ,  S₃ = S₂ – ∆₂₅×θ = 3597 – 4×18 = 3525.

                                –     –    90   8    –  

                                –    41    –    –   69     

Таблица 1.5

bj ai	68	68	90	31	87	Ui
118	15 68	16 27	14	11 23	17	10
18	15	16	13	11	14       18	12
98	21	22	16       90	16        8	23	5
110	0	0       41	0	0	0       69	26
Vj	25	26	21	21	26	S3 = 3525

Шаг 4. Проведем анализ нового опорного плана X3. Для этого плана рассчитаем потенциалы Ui и Vj и значения ∆ij. Все значения ∆ij<0, следовательно, в таблице 1.5 получен оптимальный план. 

Ответ:                                     

                                    68   27    –   23   –                   

                         X ^* =     –     –     –    –   18    ,  S ^*  = 3525.

                                –     –    90   8    –  

                                –    41    –    –   69     

Экономическая интерпретация оптимального плана поставок продукции

В результате решения транспортной задачи получен оптимальный план перевозок X ^*, по которому следует:

1.  от первого поставщика отправить три поставки: первому потребителю поставку в размере 68 единиц, второму – 27 единиц и четвертому – 23 единицы;

2.  от второго поставщика отправить пятому потребителю поставку в размере 18 единиц;

3.  от третьего поставщика направить третьему потребителю 90 единиц и четвертому – 8 единиц.

Транспортные затраты S^* на этом плане равны 3525 денежных единиц.

Замечание. Поставок  от четвертого поставщика фактически не существует, поскольку четвертый поставщик является фиктивным. Однако их наличие означает, что второй потребитель недополучит 41 единицу, а спрос пятого потребителя не будет удовлетворен на 69 единиц.

2. Задача о распределении механизмов между участками

Имеются четыре типа механизмов: Механизм 1, Механизм 2, Механизм 3 и Механизм 4, которые необходимо распределить между тремя участками работ A, B и C. Количество механизмов каждого типа составляет 74, 53, 45 и 24 штуки соответственно. Известны потребности в механизмах каждого участка: 90, 61 и 45 штук, а также производительность каждого типа механизма на каждом участке работ (в единицах работы/единицу времени).

Исходные данные задачи представлены в нижеследующей таблице.

Тип механизма	Производительность на участке			Парк механизмов	Спрос участка
	A	B	C
Механизм 1	3	5	3	74	Уч-ка A     90
Механизм 2	7	3	7	53	Уч-ка B     61
Механизм 3	6	3	5	45	Уч-ка C     45
Механизм 4	8	5	5	24

Требуется найти такое распределение механизмов между участками работ, при котором их суммарная производительность является максимальной.

Решение

Задача о распределении механизмов между участками работ по своему характеру не имеет ничего общего с транспортировкой груза, однако ее можно представить как задачу транспортного типа.

Пусть x_ij – количество механизмов i-го вида, распределенное на j-й участок работы. Известны величины c_ij – производительность i-го механизма при работе на j-м участке.

Проведем аналогию данной задачи с транспортной задачей. Поставщики и объемы их производства в транспортной задаче – это типы механизмов и их наличное количество, потребители и объемы их потребностей – это наименования участков и их потребности в определенном количестве механизмов.

В задаче о распределении механизмов по участкам работ ставится цель: максимизировать суммарную производительность всех механизмов, работающих на участках. Сама целевая функция S имеет вид:

S = 3x₁₁ + 5x₁₂ + 3x₁₃ + 7x₂₁ + 3x₂₂ + 7x₂₃ + 6x₃₁ + 3x₃₂ + 5x₃₃ + 8x₄₁ + 5x₄₂ + 5x₄₃.

В транспортной задаче целевая функция минимизируется. Поэтому, чтобы решить рассматриваемую задачу как транспортную, нужно умножить все значения коэффициентов функции S (производительностей механизмов) на -1. Целевая функция примет вид: 

P = -S = -3x₁₁ – 5x₁₂ – 3x₁₃ – 7x₂₁ – 3x₂₂ – 7x₂₃ – 6x₃₁ – 3x₃₂ – 5x₃₃ – 8x₄₁ – 5x₄₂ – 5x₄₃

и нужно будет найти ее минимум.

Проверим, является ли рассматриваемой задача закрытой. Для этого вычислим общее количество механизмов:  = 196 и потребности всех участков работ в механизмах: 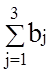=196. Так как 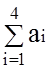=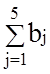, то задача является закрытой.

Экономико-математическая модель задачи имеет вид:

                                             x₁₁ + x₁₂ + x₁₃               = 74,                                              (2.1)