Решение задач линейного программирования транспортного типа: Методические указания к выполнению индивидуальных домашних заданий, страница 2

Нахождение начального опорного плана может осуществляться различными способами. Наиболее простыми в использовании являются метод северо-западного угла и метод минимального элемента.

При проверке на оптимальность допустимого плана используется следующий критерий.

Теорема 2. Допустимый план перевозок X^* = () в транспортной задаче будет оптимальным тогда и только тогда, когда найдутся числа u₁,…, u_m и v₁, …,v_n такие, что выполнены следующие соотношения:

                                                     v_j –  u_i ≤ с_ij   для всех i, j                                                                                                   (6)

                                                     v_j –  u_i = с_ij, если > 0.(7)

Числа u_i называются потенциалами пунктов отправления, а v_j — потенциалами пунктов назначения. Условия (6) и (7) означают, что разность потенциалов между двумя любыми пунктами отправления и назначения в оптимальном плане не должна превосходить затрат на перевозку единицы груза. Если же между пунктами осуществляется перевозка, то разность потенциалов между ними в точности равна затратам на перевозку единицы груза. Потенциалы могут интерпретироваться как цены продукции в этих пунктах.

С помощью этого критерия можно не только проверить на оптимальность любой план перевозок, но и указать способ улучшения неоптимального плана. Для этого обычно используется метод потенциалов, который представляет собой модификацию симплекс-метода, учитывающую специфику транспортной задачи.

2. Методические указания по решению задач транспортного типа

1. Задача о перевозке груза (транспортная задача)

В трех пунктах производства производится некоторый продукт в количествах а₁ = 118, а₂ = 18, а₃ = 98 единиц соответственно. Этот продукт необходимо доставить в пять пунктов потребления, заявки которых составляют b₁ = 68, b₂ = 68, b₃ = 90, b₄ = 31, b₅ = 87 единиц соответственно.

Известны транспортные расходы (тарифы) c_ij (i = , j = ) на перевозку единицы продукции от i-го поставщика j-му потребителю:

                                   

                                                        15   16   14   11   17          

                                              С =    15   16   13   11   14                                                                                    

                                                              21   22   16   16   23   .              

Требуется найти план перевозок продукции, при котором суммарные транспортные расходы будут минимальными.

Решение

Решение любой транспортной задачи должно начинаться с проверки того, выполняется ли условие ее закрытости, гарантирующее существование оптимального плана перевозок. Для нашей задачи это условие имеет вид: = .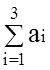

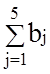Вычислим 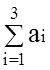= 118 + 18 + 98 = 234 и 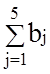= 68 + 68 + 90 + 31 + 87 = 344.

Так как 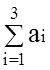 < 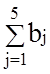, то исходная транспортная задача не является закрытой. Прежде чем приступить к нахождению оптимального плана перевозок, нужно сделать ее закрытой. Для этого следует выполнить такие действия:

1.  Ввести четвертого (фиктивного) поставщика с объемом предложения
а₄ = 344 – 234 = 110 единиц;

2.  Положить транспортные тарифы на перевозку грузов от этого поставщика
ко всем потребителям равными нулю, т. е. с_4j = 0, j = .

Замечание. Если окажется, что  > , то в исходной задаче следует ввести шестого (фиктивного) потребителя с заявкой b₆ =  –  и положить тарифы на перевозку грузов от всех поставщиков к этому потребителю равными нулю, т. е. с_i6 = 0, i = .

После добавления фиктивного поставщика получена закрытая транспортная задача, в которой число поставщиков m = 4, а число потребителей n = 5. Обозначим х_ij – объем поставки от i-го поставщика к j-му потребителю (i = , j = ). Тогда модель новой транспортной задачи имеет вид:

                                   x₁₁ + x₁₂ + x₁₃  + x₁₄ + x₁₅ = 118,                                              (1.1)

                                   x₂₁ + x₂₂ + x₂₃  + x₂₄ + x₂₅ = 18,                                                (1.2)

                                   x₃₁ + x₃₂ + x₃₃  + x₃₄ + x₃₅ = 98,                                                (1.3)

                                    x₄₁ + x₄₂ + x₄₃  + x₄₄ + x₄₅ = 110,                                              (1.4)

                                     x₁₁ + x₂₁ + x₃₁  + x₄₁               = 68                                                (1.5)

                                    x₁₂ + x₂₂ + x₃₂  + x₄₂               = 68                                                (1.6)

                                    x₁₃ + x₂₃ + x₃₃  + x₄₃               = 90                                                (1.7)

                                    x₁₄ + x₂₄ + x₃₄  + x₄₄               = 31                                                (1.8)

                                   x₁₅ + x₂₅ + x₃₅  + x₄₅          = 87                                                (1.9)

                                         х_ij  0, i = , j =.                                                    (1.10)

  S = 15x₁₁ + 16x₁₂ + 14x₁₃ + 11x₁₄ + 17x₁₅ + 15x₂₁ + 16x₂₂ + 13x₂₃ + 11x₂₄ +                 

        + 14x₂₅ + 21x₃₁ + 22x₃₂ + 16x₃₃ + 16x₃₄ + 23x₃₅ → min.                                (1.11)

Для нахождения оптимального плана этой задачи ее следует представить в виде транспортной таблицы (см. табл. 1.0), строки которой соответствуют поставщикам, а столбцы – потребителям.

Таблица 1.0

bj ai	68	68	90	31	87
118	15   x11	16   x12	14   x13	11   x14	17   x15
18	15   x21	16   x22	13   x23	11   x24	14   x25
98	21   х31	22   х32	16   x33	16   х34	23   x35
110	0   х41	0   х42	0   х43	0   х44	0   х45