Физика: Методические указания к лабораторным работам (Эффект Холла в полупроводниках . Измерение температуры нагретых тел с помощью радиационного пирометра. Изучение работы оптического квантового генератора (лазера). Исследование люминесценции кристаллофосфоров)

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Кафедра «Физика-2»

ФИЗИКА

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К ЛАБОРАТОРНЫМ РАБОТАМ 47, 50, 52, 55, 55к, 147, 150, 151

МОСКВА - 2008

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Кафедра «Физика-2»

ФИЗИКА

Рекомендовано редакционно-издательским советом университета

в качестве методических указаний для студентов специальностей

ИУИТ, ИСУТЭ, ИЭФ, ИТТОП, вечернего факультета

Под редакцией профессора С.М. Кокина и профессора В.А. Никитенко

МОСКВА - 2008

УДК 53

К-59

Физика: методические указания к лабораторным работам 47, 50, 52, 55, 55к, 147, 150, 151/ Под ред. проф. С.М. Кокина, проф. В.А. Никитенко. – переизд., доп. – М.: МИИТ, 2008. – 95 с.

Методические указания содержат описания лабораторных работ по общему курсу физики, предназначенных для студентов первого и второго курсов ИУИТ, ИСУТЭ, ИЭФ, ИТТОП, вечернего факультета.

©  Московский  государственный

университет путей сообщения

(МИИТ), 2008

Работа 47

ЭФФЕКТ ХОЛЛА В ПОЛУПРОВОДНИКАХ

Цель работы. Измерение холловской разности потенциалов в полупроводниковой пластине и определение концентрации, подвижности и знака носителей заряда, участвующих в токе.

Введение

Эффект Холла заключается в возникновении поперечной разности потенциалов при пропускании тока через металлическую или полупроводниковую пластинку, помещенную в магнитное поле, направленное под некоторым углом к направлению тока. Обычно вектор индукции магнитного поля  направляют перпендикулярно вектору плотности тока .

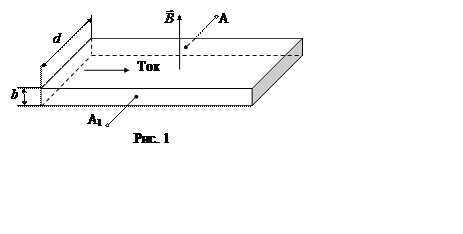
Разность потенциалов возникает, как это показано на рис. 1, между точками А и А₁, лежащими на прямой, перпендикулярной как к вектору, так и к вектору индукции . В отсутствие магнитного поля точки А и А₁ лежат на эквипотенциальной поверхности.

Классическая электронная теория объясняет эффект Холла следующим образом: поток электрических зарядов, попадая в магнитное поле, отклоняется от первоначального направления своего движения под действием силы Лоренца

 = q[],                                            (1)

где q– величина заряда,  – средняя дрейфовая скорость.

При этом одна из боковых сторон пластинки получает отрицательный заряд, в то время как противоположная сторона заряжается равным ему по величине положительным зарядом. Накопление зарядов происходит до тех пор, пока сила, действующая на электрический заряд со стороны холловского электрического поля, не уравновесит силу Лоренца:

q + q[] = 0.                                        (2)

Таким образом, напряженность поперечного холловского электрического поля

 = - [].

Если векторы  и  взаимно перпендикулярны, то напряженность поперечного электрического поля равна по абсолютной величине E = u_dB, u_d = ïï, что соответствует поперечной разности потенциалов:

U_H = Ed = u_dBd,                                          (3)

где d – расстояние AA₁ (см. рис. 1).

Средняя скорость направленного движения носителей тока связана с плотностью тока j соотношением j = nqu_d, где п – концентрация носителей заряда (число носителей в единице объема, q– заряд носителя). Следовательно,

u_d = .                                                 (4)

Выразив плотность тока через силу тока I:

j = ,                                                     (5)

(b – толщина пластины) и подставив выражения (5) и (4) в (3), получим

U_H =  = R_H,                                         (6)

где

R_H = .                                                    (7)

КоэффициентR_H называют постоянной Холла.

Формула (7) получается без учета закона распределения электронов по скоростям. Более точный расчет с учетом закона распределения носителей по скоростям в рамках классической статистики приводит к выражению для постоянной Холла

R_H = A.                                              (8)

Для атомных полупроводников, например, для кремния, A = 3p/8.

Для полупроводников с ионной связью, к которым относится рассматриваемое в данной работе интерметаллическое соединение арсенид галлия, A = 1. В этом случае применима формула (7).

Соотношение (6) позволяет определить постоянную Холла R_H, м³/Кл, и концентрацию носителей заряда n, м^-3 , в образце из опытных данных

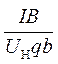R_H = ;     n = .                                  (9)

Если R_H известно, то, измеряя U_H и I, можно найти В. Этот способ измерения B используется в технике (датчики Холла).

Важной характеристикой полупроводника является подвижность в нем носителей заряда, под которой подразумевается средняя скорость, приобретаемая носителем в поле, напряженность которого равна единице. Если в поле напряженностью E носители приобретают скорость u_d, то подвижность их u, м²/(В×с), равна

u = .                                               (10)

Используя связь между плотностью тока, напряженностью электрического поля и проводимостью j = sE и учитывая (4) и (10), можно выразить подвижность через проводимость s и концентрацию носителей заряда:

u = .                                             (11)

Из соотношений (7) и (11) следует

u = R_Hs.                                             (12)

Таким образом, для определения подвижности носителя  необходимо измерить R_H и s.

Знак постоянной Холла определяется знаком носителей заряда. У полупроводников постоянная Холла может быть отрицательной и положительной, так как существует два типа проводимости. У полупроводников с электронной проводимостью (полупроводников n-типа) перемещаются электроны, и знак постоянной Холла отрицателен. У другого типа полупроводников электропроводность осуществляется положительными зарядами или так называемыми «дырками». Такие полупроводники называются дырочными (полупроводниками р-типа). Они имеют положительный знак постоянной Холла. При этом ïq_nï = q_p = e.

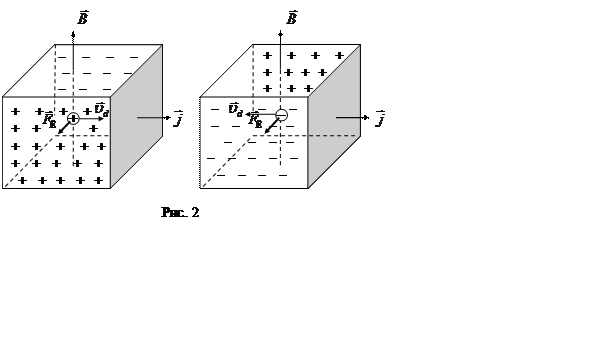Направление силы Лоренца изменяется на противоположное как при изменении направления движения зарядов, так и при изменении их знака. Следовательно, при одинаковом направлении тока и магнитной индукции B сила Лоренца, действующая на положительные и отрицательные носители, имеет одинаковое направление. Поэтому в случае положительных носителей потенциал верхней грани (см. рис. 2) выше, чем нижней, а в случае отрицательных носителей – ниже. Таким образом, определив знак холловской разности потенциалов, можно установить знак носителей заряда, участвующих в токе.