Физика: Методические указания к лабораторным работам (Эффект Холла в полупроводниках . Измерение температуры нагретых тел с помощью радиационного пирометра. Изучение работы оптического квантового генератора (лазера). Исследование люминесценции кристаллофосфоров), страница 19

u_Д = еE t/m                                         (1)

Если для потери электроном приобретённой скорости достаточно одного столкновения, то

t ,                                                 (2)

где u = u_Т + u_Д – полная скорость электрона, складывающаяся из тепловой u_Т и дрейфовой u_Д, l – расстояние, которое пролетает электрон от одного столкновения до другого.

Как мы говорили выше, обычно u_Т >> u_Д, и поэтому, следуя классической теории электропроводности, можно записать, что, поскольку u_Т » u_КВ, то

u_Д = еEl/(mu_КВ) = 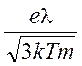E.                            (3)

Теперь запишем формулу для силы тока I, проходящего по проводнику.

Если за время Dt по проводнику, имеющему длину l и площадь поперечного сечения S, проходят N электронов (каждый из которых имеет заряд е), общая сила тока через образец будет равна

I =  =  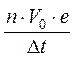= nqS = enu_ДS.

Здесь n - концентрация электронов в проводнике; V₀ = lS - его объем.

Разделив обе части равенства на S, получим для плотности тока

j =  = еnu_Д.                                       (4)

Но согласно закону Ома

j = sE,                                               (5)

где E - напряженность электрического поля; s - удельная электропроводность проводника, которая может быть выражена через его удельное сопротивление r:  s = 1/r (единица измерения удельной электропроводности - сименс на метр; очевидно, что 1 См×м^-1 = 1 Ом^-1×м^-1).

Введём обозначение:

u = u_Д/E;                                             (6)

параметр u называется подвижностью электронов. В итоге на основании уравнений (3) – (5) можно записать:

s = еnu,                                               (7)

r = 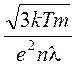.                                          (8)

Поскольку электрическое сопротивление R ~ r (в частности, для цилиндрического проводника R = r), из соотношения (8) следует, что R должно быть прямо пропорционально корню квадратному из температуры: R ~  (или R ~ , где температура t выражена в градусах Цельсия).

На практике, однако, зависимость R(t) для металлов имеет вид

R = R₀(1 + at),                                        (9)

где a - температурный коэффициент сопротивления, параметр, который зависит от свойств материала; R₀ - сопротивление образца при 0°С.

Очевидно, что зависимость (9) отличается от той, которую предсказывает теория.

В случае полупроводников разница между теорией и экспериментом оказывается еще более разительной. Так, измерения показывают, что для собственных (не содержащих примесей) полупроводников

R » C×exp[E/(2kT)],                                  (10)

где С – коэффициент, слабо зависящий от температуры; E – характерная энергия (обычно составляющая от десятых долей до нескольких электронвольт), величина которой определяется природой полупроводника).

Объяснение наблюдаемых в эксперименте зависимостей R(Т) и s(Т) для металлов и полупроводников явилось одним из достижений теории электропроводности, построенной с применением методов квантовой статистики. В основе объяснения лежит анализ температурного поведения сомножителей, входящих в формулу (7): концентрации свободных носителей заряда n и их подвижности u.

В металле ускориться электрическим полем способны лишь электроны, имеющие максимальные значения энергии (максимальная энергия Е_F, которую имеют электроны в металле при 0 К называется энергией Ферми). Число таких электронов (и, следовательно, их концентрация n) в металле практически не меняется вплоть до температуры плавления, и именно поэтому на вид зависимости s(Т) главное влияние оказывает то, каким образом изменение температуры сказывается на подвижности электронов u.

Характер поведения функции u(T) определяется разными факторами, одни из которых способствуют увеличению подвижности, а другие – её уменьшению. Наиболее существенными из них являются рассеяние носителей заряда (в металлах – электронов, в полупроводниках – электронов и дырок) на заряженных точечных дефектах кристаллической решетки проводника (в частности – на ионах примесей) и рассеяние на колеблющихся атомах самой кристаллической решетки. Поскольку подвижность определяется скоростью u_Д направленного движения носителей заряда, любое отклонение направления вектора скорости от направления силовых линий означает уменьшение u.

I. Область низких температур

При низких температурах заряженные точечные дефекты, мимо которых пролетает электрон, действуют на него, меняя траекторию движения. Электрон отклоняется от первоначального направления движения, следовательно, его средняя скорость в этом направлении падает. Однако, чем выше скорость электрона, тем легче он проскакивает мимо подобных дефектов, и они не успевают заметно изменить направление его движения, задаваемое силовыми линиями электрического поля. Повышение Т как раз и означает увеличение не только тепловой (u_Т ~ ), но и общей скорости u = u_Т + u_Д носителей заряда, то есть с ростом температуры подвижность электронов при данном механизме рассеяния будет увеличиваться.

Расчёты показывают, что при рассеянии на заряженных примесях свободных электронов (и дырок) в невырожденном полупроводнике (поведение таких носителей заряда описывается статистикой Максвелла - Больцмана) зависимость подвижности от температуры должна иметь следующий вид:

u(Т) ~ T^3/2;                                          (11)

эксперимент подтверждает данный вывод.

В металле, поведение электронов которого описываемого статистикой Ферми-Дирака, кинетическая энергия и скорость тех электронов, которые участвуют в создании электрического тока, практически не зависят от температуры (энергия этих электронов называется энергией Ферми, а соответствующая скорость обозначается символом u_F):

u = u_F + u_Д;

u » Const.                                          (12)

II. Область высоких температур